风险元概率估计与相关分析

使用上述风险元传递函数在分析实际问题的时候，还需要进行风险元的概率估计和风险元的相关分析，在此基础上，针对具体的问题进行具体分析。

1.风险元的概率估计

风险元的概率估计主要包括找出风险元变化的原因、风险元变化的概率分布特征参数等内容，给出风险元变化的大小及其可能性。例如，某水力发电厂年发电量的变化可以用概率分布作出定量估计。定量估计的方法有主观估计法和客观估计法。

主观估计是专家根据长期积累的各方面的经验及当时搜集到的历史数据为基础所做出的估计，这种估计，带有一定的偏差，为了减小这种偏差，美国著名咨询机构兰德公司于20世纪50年代初曾发明了一种名叫特尔斐（Delphi）的方法。特尔斐方法就是将许多专家的意见相互独立地集中起来，充分发挥信息反馈和信息控制的作用，使分散的评估意见逐次收敛，最后集中在协调一致的评估结果上，这比某一个人的意见接近客观实际的概率要大，因此，用特尔斐方法来估计各风险变量的大小及其可能性是切实可行的方法之一。

客观估计法实际上是依据现有的各种数据和资料对未来事件发生的可能性进行预估。客观估计的方法很多，如预测技术中的时间序列分析法、趋势外推法、类推法、回归分析法、神经网络等。

由于影响项目目标的各风险元的变化是随机的（只考虑客观风险元），在项目管理过程中，决策者难以掌握和控制它的变化。即使依据大量类似项目的历史统计资料，也难以预测未来事件的变化，这就需要引用概率分布来描述各风险元的变化规律。在广义项目管理的风险元概率估计中常用的概率分布有正态分布、均匀分布、三角形分布、梯形分布、二项分布等。

由于各建设项目的时间、地点和涉及的政治、社会、经济、技术、环境因素等方面的差异，很难单纯利用客观估计的方法给出风险元的概率分布，多数情况下需要借助主观估计的数据。单纯的主观估计也不可能给出风险元准确完善的概率分布。通常是根据信息情况和精度要求，分析风险元的变化特性。一般情况下可以进行如下几种类型的估计：

（1）二点估计。若估计出风险元的变化范围为[a，b]，且变化是等可能的，则用均匀分布来描述；若可以判断出变量在此范围内均值出现的可能性最大，则利用正态分布来描述，如图3.1所示。

（2）三点估计。若给出了风险元最低的、最可能出现的和最高的三个估计值，这种估计实质上是给出了风险元的三角形分布或β分布，分别如图3.2或图3.3所示。

（3）四点估计。若估计出风险元正常情况下在c、d之间变动，极端情况下会波动在a、b之间，这种估计实质上是给出了风险元的梯形分布，如图3.4所示。

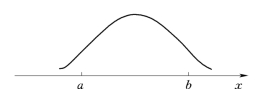
图3.1　正态分布概率密度示意图

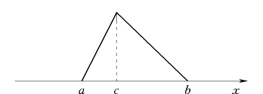
图3.2　三角形分布概率密度示意图

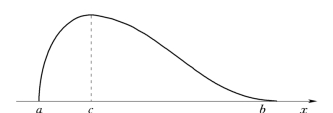
图3.3　β分布概率密度示意图

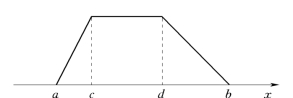
图3.4　梯形分布概率密度示意图(www.xing528.com)

在这里，风险元概率分布的确定，并不需要给出它的分布函数，只需要给出概率分布的数字特征期望值E（X）和方差D（X）即可，其值归纳见表3.1。

表3.1　不同分布概率分布数字特征计算公式

三角形分布与均匀分布实质上是梯形分布的特例，当梯形分布的c点与d点重合时，变为三角形分布；当a与c重合、d与b重合时变为均匀分布。

在资料与数据不足的情况下，不可能得知风险元的真实分布时，有经验的专家或专家组还是能够比较正确地将风险元概率分布概化为上述各种分布、并估计出上述各特征值。这些分布已经考虑了风险出现的各种信息，为实现风险元的传递计算奠定了必要的基础。

2.风险元的相关分析

设影响项目目标的风险元为X1，X2，…，Xn，风险元的相关分析就是要定量分析它们之间的相互影响程度，定量分析的指标是相关系数ρ，通常情况下，相关系数的确定有如下几种方法。

（1）主观判断法。通过分析两风险元之间有无联系来确定。若两风险元之间没有联系或联系甚微，取ρ＝0；若联系比较密切，则可取0.5≤|ρ|≤1.0。

（2）客观估计法。若历史统计资料较多，可直接点绘Xi与Xj的相关图，如图3.5所示，然后作平行于纵轴的直线A将点阵左右均分，再作平行于横轴的直线B将点阵上下均分，这样直线A、B将点阵分为四部分，若右上、左上、左下、右下的点数分别为k1、k2、k3、k4，则：

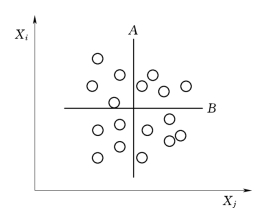
图3.5　风险元的相关分析示意图

如果Xi与Xj的成对点据有多组，则可按下式直接计算：

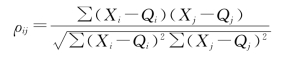
式中：Qi、Qj分别为变量Xi、Xj的数学期望。

ρij确定后，为表达清晰，可写成相关系数矩阵的形式：

式中：ρ11＝ρ22＝…＝ρnn＝1。