风险元传递理论的概率论基础

当风险元具有随机变化特征时（即随机风险元），则可以利用概率论中随机变量的相关理论对风险元的传递进行相关的分析和计算。而依照概率论的知识，又可将风险元分为离散型风险元和连续型风险元两种。

1.离散型随机风险元的分布函数

假设离散型风险元X的所有可能取值为xk（k＝1，2，…），则风险元X的分布律（也可称为概率函数）可以表示为：

P{X＝xk}＝pk（k＝1，2，…）

其中　

而离散型风险元X的分布函数可以表示为：

假设X和Y为两个离散型风险元，则X和Y的联合分布律（概率分布）可以表示为：

其中　pij≥0并且

而X和Y的联合分布函数可以表示为：

2.连续型随机风险元的分布函数

假设X是一个连续型风险元，则其分布函数可以表示为：

式中：连续函数f（t）称为F（x）的概率密度函数。

假设X和Y为两个连续型风险元，则X和Y的联合分布函数可以表示为：

3.随机风险元的数字特征

（1）数学期望（均值）。数学期望反映了随机风险元变化的分布中心。离散型风险元X的数学期望E（X）如式（2.34）所示；而连续型风险元X的数学期望E（X）如式（2.35）所示。

对于数学期望，有以下4条性质：

1）设C是常数，则有E（C）＝C。

2）设X是一个风险元，C是常数，则有E（CX）＝CE（X）。

3）设X和Y为两个风险元，则有E（X+Y）＝E（X）+E（Y）。

4）若X和Y为两个相互独立的风险元，则有E（XY）＝E（X）E（Y）。

（2）方差。若X是一个随机风险元，若式（2.36）存在，则称式中的D（X）为X的方差，即：

当连续型随机风险元X有概率密度函数f（x）时，其方差为：

当离散型随机风险元X有概率函数pk时，其方差为：

此外，也可按照式（2.39）计算风险元X的方差：

随机风险元的方差直接反映了风险元变化的不均匀程度，不均匀程度的大小反映了风险的大小。在关系型风险元传递计算中，通过方差公式来描述风险元的传递特性是风险传递理论的主要方法之一。

方差具有以下几条性质：

1）设C是常数，则有D（C）＝0。

2）设X是一个随机风险元，C是常数，则有D（CX）＝C2D（X）。

3）若X和Y为两个风险元，有D（X+Y）＝D（X）+D（Y）+2Cov（X，Y），其中：(www.xing528.com)

Cov（X，Y）＝E{[X-E（X）][Y-E（Y）]}＝E（XY）-E（X）E（Y）

4）如果x1，x2，…，xn相互独立，则：

特别地，若X和Y为两个相互独立的随机风险元，则：D（X+Y）＝D（X）+D（Y）。

（3）标准差（或称均方差）。式（2.41）中的σ（X）称为随机风险元X的标准差。

4.可信度

在概率论中，设总体X的分布函数F（x，θ）含有一个未知参数θ，θ∈Θ，（Θ是θ的可能取值范围），对于给定值α（0＜α＜1），若由样本X1，X2，…，Xn确定的两个统计量＝（X1，X2，…，Xn）和＝（X1，X2，…，Xn）（θ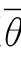＜），对于任意θ∈Θ满足：

则称随机区间是θ的置信水平为1-α的置信区间，和分别称为置信水平为1-α的双侧置信区间的置信下限和置信上限，1-α称为置信水平。

定义2.7　在风险元传递理论中，若将总体X看成是随机风险元时，称置信水平1-α为随机风险元总体X的可信度。

5.区间数

当风险元具有模糊性质的时候，可以利用区间数或者模糊数学的相关理论对风险元传递方式进行计算。由于模糊隶属函数可以通过模糊数学中λ-截集将模糊数转化成一系列关于λ-截集上的区间数进行研究，因此，可以说区间数是一种特殊的模糊数。

定义2.8（区间数的定义）　若R是实数集，对任意的a-，a+∈R，如果a-≤a+，则称闭区间a∈[a-，a+]＝{x：x∈R，a-≤x≤a+}为一个区间数风险元x，其区间宽度定义为：W[a-，a+]＝a+-a-。

（1）区间数的基本运算。设c为常数，xa＝[a-，a+]、xb＝[b-，b+]表示两个区间数风险元，则有如下的运算法则：

其基本逻辑运算如下：

式中：∧、∨分别表示逻辑和、逻辑积运算。

（2）区间数的比较规则。设两个区间数a＝[a-，a+]、b＝[b-，b+]，当a-＝b-、a+＝b+时，称a和b相等，记做a＝b。

定义2.9（区间数可能度的定义）　当a、b同时为区间数或者有一个为区间数时，设a＝[a-，a+]，b＝[b-，b+]，w（a）＝a+-a-，w（b）＝b+-b-，则a≥b的可能度可由式（2.48）计算。

由此可以得出如下性质及推论：

性质2.1　Pa≥b+Pb≥a＝1。

性质2.2　若b-＜a-＜b+＜a+，有0.5＜Pa≥b＜1。

性质2.3　在a-≤b-＜b+＜a+情况下，若a+-b+＝b--a-，有Pa≥b＝0.5；若a+-b+＞b--a-，有Pa≥b＞0.5；若a+-b+＜b--a-，有Pa≥b＜0.5。若将条件和推论互换，依然成立。

性质2.4　设a＝[a-，a+]，b＝[b-，b+]，c＝[c-，c+]，若Pa≥b＞0.5；Pb≥c＞0.5，则Pa≥c＞0.5。该性质也称为传递性。

推论2.1　对于两个区间数的中点a0、b0，若a0＝b0，有Pa≥b＝0.5；若a0＞b0，有Pa≥b＞0.5；若a0＜b0，有Pa≥b＜0.5。反之依然成立。

证明：当a0＝b0时，有：

由性质2.3可得：Pa≥b＝0.5

因此a0＝b0⇔Pa≥b＝0.5。

同理可得a0＞b0⇔Pa≥b＞0.5；a0＜b0⇔Pa≥b＜0.5。

证毕。