扩展风险元的度量方法优化

根据不确定性信息的特点和分类，引入物理学中的“熵”的概念，对信息对应的风险元进行度量。熵的概念最先是由德国物理学家Clausius R提出的，是物理系统无序性的度量，现在被称为热熵。Shannon C E根据Neuman V的意见，把与热熵具有相同数学表达形式的“随机变量的不确定性度量”称之为熵，即概率熵（Shannon熵）。Shannon用概率论作为度量信息的数学工具，将信息定义为消除不确定性，从而把信息与不确定性关联起来，将熵作为一个度量信息状态不确定性的尺度[136-137]，由此产生了信息熵的概念，扩展了熵的应用范围。笔者利用Shannon熵的思想将风险元的传统度量进行扩展，给出如下的风险元的熵信息度量。

1.随机风险元度量

根据概率熵[137]的定义，给出随机风险元的度量公式：

式中：K为正的常数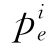；是随机风险元事件A将要发生的概率，＝1，给出由于知道事件发生的随机性而获取的平均信息。当对数底分别为2、e、10时，信息单位分别为比特（Bit）、奈特（Nat）、迪特（Dit）。对于连续变量，则可表示为：

式中：ω（x）为随机风险元的密度函数。式（2.11）可看作是离散条件下的随机风险元公式（2.10）在连续条件下的推广。由于Shannon的概率熵具有许多重要的性质，如对称性、归一性、强可加性和可扩展性等，因此随机风险元也同样具有上述性质，这将在后续各章的具体应用中得以体现。

2.模糊风险元度量

既然考虑了不确定性信息的随机性，对其模糊性也必须考虑，这样根据模糊风险元的定义，结合上述随机风险元的度量，给出如下的模糊风险元度量。

设A表示模糊风险元定义中论域S的一个模糊子集，μ为隶属函数，则：

式中：任意的模糊风险元xi属于论域S；μi的范围为[0，1]。那么模糊风险元的度量公式为：

式中：K′为归一化常数。S（μi）可以表示为：

对于连续变量，则可表示为：(www.xing528.com)

3.灰色风险元度量

根据灰色风险元的定义，设A表示灰色风险元定义中论域S′⊂S的一个灰子集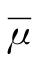，和分别为灰色风险元x的上下隶属函数，则

那么灰色风险元的度量公式为：

式中：K′为归一化常数。S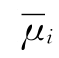（）可以表示为：

S（）的表达与式（2.19）类似，对于连续变量，则可表示为：

4.未确知风险元度量

由于未确知数学在定义形式上与概率论中的概率表述比较相似，因此在风险元的度量上，两者也比较相似，其区别在于两者所表示的实际意义和数学操作方式。未确知风险元的度量公式为：

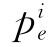式中：K为正的常数；[a，b]为未确知风险元的分布区间；F（）为未确知风险元的分布函数F（x）的取值；为风险元xi落在区间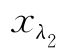（，]上的可信度；⊗符号为未确知数学中的乘法数学操作符。对于连续变量，式（2.21）可表示为：

式中：ω（x）为未确知风险元的密度函数，当分布区间[a，b]变为[-∞，+∞]时，式（2.22）变为：