传统风险元素的度量方法简析

1.结果

这种度量将风险的度量重点偏重于不确定性条件下各种可能出现的结果。例如在广义项目中的综合评价以及和经济相关的某些领域中，尽管在风险理论上承认在评价不确定性的相对重要性时，必须同时考虑后果程度和相应的发生概率两方面信息，然而在某些实际应用中往往强调后果程度，而忽视其发生概率。即这种定义强调结果，相应的风险元论域为：

U＝{c1，c2，…，cn}

相应的，其传递表达方式为：

2.不确定性

这种度量把风险视为不确定情况下各种结果中出现的可能性，例如在广义项目中对施工管理项目的自然灾害风险度量中。类似地，这种风险元的论域为：

U＝{p1，p2，…，pn}

相应的，其传递表达方式为：

3.概率与不确定性的总体表示

这种度量把风险视为不确定条件下某种可能出现的结果及其出现的可能性的某种综合，其中最常用的总体表示是概率与不确定性的乘积方式，即期望值。该度量方法是目前大多数风险评估应用中采用的风险度量方法，也是广义项目中应用最常用的风险度量方法。这种风险元的论域为：(www.xing528.com)

U＝{x1，x2，…，xn}

式中：xi＝fi（p，c）。相应的，其传递表达方式为：

4.差异性

这种度量将风险视为各种结果之间的差异，风险的高低将体现在各种结果之间的差异大小上，其度量往往采用某种距离来衡量，其中最常用的度量方式是方差。差异既可以通过结果本身或发生概率来表示，也可以用两者的总体表示来描述。该论域为：

U＝{x1，x2，…，xn}

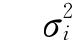其中xi＝（p） or（c）or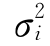[p，c，f（p，c）]

相应的，其传递表达方式为：

上述四种度量方法在目前的风险评估中都有应用，在广义项目中都有存在的合理性，都是对风险不同定义的数学刻画和归纳。应该说，在特定的情况下，各种度量都有其存在的合理理由。