新古典经济增长模型简介

早在1956年，美国经济学家索洛和斯旺就分别提出新古典经济增长模型，后来英国经济学家米德又对新古典经济增长理论作了系统的表述。新古典经济增长理论中，既有凯恩斯经济学的成分，又有凯恩斯以前的传统经济学的成分，这是它的理论特征。

1.新古典经济增长理论的假定

新古典增长模型有如下几个假定：社会只生产一种产品；社会储蓄函数为S=sY（s为储蓄率），储蓄在国民收入中所占的份额保持不变；劳动力按照一个不变的比率n增长；技术水平不变；生产的规模报酬不变；在完全竞争的市场条件下，劳动和资本是可以通过市场调节而充分地相互替代。

图13⁃2 人均生产函数曲线

根据以上六个假定，生产函数可以表示为人均形式，即

y=f（k）（13⁃16）

式中　y——人均产量；

k——人均资本量。

y=f（k）表示，人均产量取决于人均资本量，人均资本量的增加会使人均产量增加。但是，由于报酬递减规律，人均产量会以递减的速度增长。图13⁃2是生产函数的图示。

2.新古典经济增长模型的基本方程

sy=Δk+（n+δ）k（13⁃17）

这就是新古典增长模型的基本方程。

式中　sy——人均储蓄；

Δk——人均资本增量；

（n+δ）k——资本的广化。（n+δ）k由两部分组成。分解为：(www.xing528.com)

nk——人均储蓄中用于装备新增劳动力的花费；

δk——人均储蓄中用于替换旧资本的花费，即人均折旧量。

人均储蓄中超过资本的广化的部分会使得人均资本增多，即Δk>0，Δk就是资本的深化。因此，新古典增长模型的基本方程可以表述为：人均储蓄是资本深化与资本广化之和，或者说，人均储蓄用于资本深化与资本广化两部分。

3.稳态分析

稳态是指一种长期稳定、均衡的状态，是人均资本与人均产量达到均衡数值并维持在均衡水平不变。在稳态下，k和y达到一个持久的水平。这就是说，要实现稳态，资本的深化为零，即人均储蓄全部用于资本的广化。因此，稳态条件是：sy=（n+δ）k。稳态时，Δk=0。

虽然在稳态时y和k的数值不变，但总产量Y与总资本存量K都在增长。由于 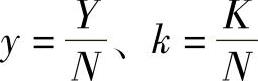，所以，总产量Y与总资本存量K的增长率必须与劳动力数量N的增长率n相等。这就是说，在稳态时，总产量与总资本存量的增长率相等，且都与劳动力的增长率n相等，即

还可以用图形来分析稳态，如图13⁃3所示。

由于0<s<1，故储蓄曲线sy与人均生产函数曲线y的形状相同且位于y的下方。资本广化曲线（n+δ）k是通过原点、向右上方倾斜的直线。

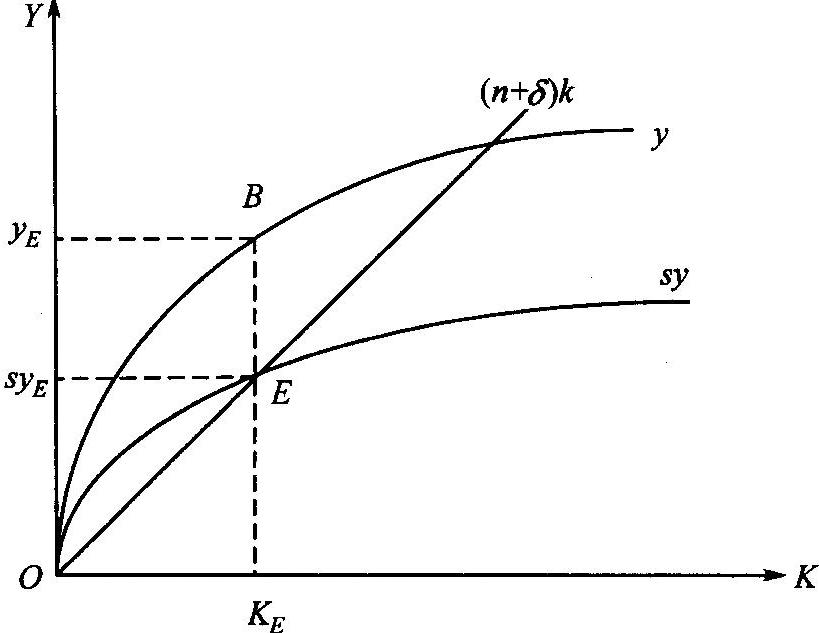
图13⁃3　经济增长的稳态

由于sy=（n+δ）k是稳态条件，所以稳态时，sy曲线与（n+δ）k曲线一定相交，交点是E点。稳态时的人均资本为k_E，人均产量为y_E，人均储蓄量为sy_E。此时，sy_E=（n+δ）k_E，即人均储蓄正好全部用来为增加的劳动力购买资本品（花费为nk_E）和替换旧的资本品（花费为δk_E），人均资本没有变化（即Δk=0）。

从图13⁃3中可以看到，在E点之左，sy曲线高于（n+δ）k曲线，表明人均储蓄大于资本广化，存在着资本深化即Δk>0。这时，人均资本k有增多的趋势，k会逐步地增加，逐渐接近于k_E。当k=k_E时，经济实现稳定状态。反之，在E点之右，人均储蓄小于资本广化，即sy<（n+δ）k，此时有Δk<0，人均资本k有下降趋势。人均资本k的下降会一直持续到k_E的数量上，达到稳态。

以上论述表明，当经济偏离稳定状态时，无论是人均资本过多还是过少，经济都会在市场力量的作用下恢复到长期、稳定、均衡状态。

显然，新古典增长模型“稳定、均衡”的结论与哈罗德⁃多马经济增长模型“稳定、均衡的极小可能性及经济的剧烈波动”的结论存在着重大差别。