非合作博弈论简介

非合作博弈论有四种类型，这四种类型是从两个角度形成的：

第一个角度，如果从参与人行动的先后顺序分，博弈可以划分为：静态博弈和动态博弈。所谓静态博弈，是指在博弈中，参与人同时选择行动或虽非同时但后行动者并不知道前行动者采取了什么具体行动。所谓动态博弈，是指参与人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。

第二个角度，如果从参与人对有关其他参与人（对手）的知识（对手的特征、战略空间及支付函数）的掌握程度分，博弈可以划分为：完全信息博弈和不完全信息博弈。所谓完全信息是指每一个参与人对所有其他参与人（对手）的特征、战略空间及支付函数有准确的知识。反之则为不完全信息。

将上述两个角度的划分结合起来，就得到四种不同类型的博弈：完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈。与这四种不同类型的博弈相对应的均衡概念分别是：纳什均衡、子博弈精炼纳什均衡、贝叶斯纳什均衡、精炼贝叶斯纳什均衡。这四种类型的划分、对应的均衡概念及主要代表人物可以从表5⁃2中体现出来。

表5⁃2 博弈的分类、对应的均衡概念及主要代表人物

下面，我们具体来了解这四种类型的博弈。

1.完全信息静态博弈——纳什均衡

纳什均衡指的是这样一种战略组合：这种战略组合由所有参与人的最优战略组成，也就是说，在给定别人战略的情况下，没有任何单个参与人有积极性选择其他战略，从而没有任何人有积极性打破这种均衡。

对纳什均衡概念的理解，我们可以通过分析“一个不具有法律效力的协议的执行情况”来进行。前面我们已经分析到，在相互关联的经济主体之间，如果各主体互相达成了一个具有法律约束力的协议，那么这种博弈是合作博弈。而如果各主体互相达成的协议不具有法律约束力，则这种博弈是非合作博弈。那么，在这种非合作博弈中，这个不具有法律约束力的协议是否能够自动实施呢？如果它能自动实施，则说明它构成一个纳什均衡；如果它不能自动实施，则说明它不构成一个纳什均衡。能用于分析纳什均衡的例子有许多，下面通过两个经典案例来说明。

案例5⁃1 囚徒的困境

一桩严重的杀人案在某市发生了，警察很快在附近抓到两个嫌疑犯。事实上，正是这两人合作谋划和实施了这起杀人案。但是，由于犯罪分子的犯罪手段高明、隐蔽，警方没有掌握足够的证据，只得把他们隔离囚禁起来，要求他们坦白交代。如果他们都承认杀人，每人将被判入狱15年；如果他们都不承认，每人将只被判入狱1年；如果一个抵赖而另一个坦白并且愿意出来作证，那么抵赖者将被判入狱20年，坦白者将被宽大处理——判5年，但监外执行，即不入狱。这两个囚徒该怎样做出对自己最有利的选择呢？是抵赖？还是坦白？这让两个囚徒犯难了。这就是博弈论中著名的“囚徒困境”。如果我们把囚徒双方分别称为A和B。那么，AB双方的支付矩阵如图5⁃19所示。

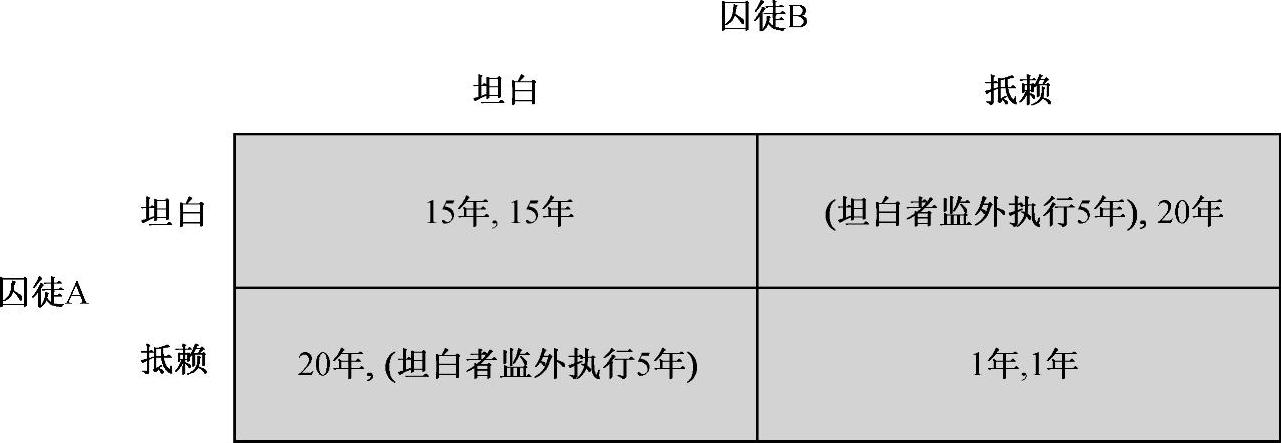
图5⁃19 囚徒的困境

从图5⁃19中可知，最好的策略是双方都选择抵赖，结果是大家都被判入狱1年。那么，双方选择的结果是否是这样的呢？我们来分析图5⁃19，现在假定两个囚徒（A、B）都是只为了自己利益打算的所谓“理性主体人”，那么，结果会怎样呢？在A看来，在B选择抵赖的情况下，A选择坦白的话，A将被判监外执行5年；但是，如果A也选择抵赖的话，将被判入狱1年。两相比较，A认为选择坦白对自己更有利。在B选择坦白的情况下，A也选择坦白的话，两个人都要坐15年牢；但是，如果A选择抵赖的话，可要坐20年牢，两相比较，A认为还是选择坦白对自己更有利。可见，不管B采取什么策略，A认为选择坦白总是对自己更有利。同样，B也会做出这样的判断和选择。可见，（坦白，坦白）即（15，15）是一个纳什均衡，是必然出现的结果，而（抵赖，抵赖）即（1，1）则不是纳什均衡，它不会是双方选择的最终结果。这是因为两个囚徒都处于被隔离的情况下无法串供，每一个人都是从利己的目的出发，每一方在选择策略时都只选择对自己最有利的策略，而不考虑任何其他对手的利益或社会福利，但选择这种策略得出的结果又适得其反。(www.xing528.com)

囚徒困境反映出一个很深刻的问题，这就是个人理性与集体理性的矛盾。如果两个人都抵赖，各判刑1年，显然比两个人都坦白各判15年要好。但这个结果不可能出现，因为它不满足个人理性要求，（抵赖，抵赖）不是纳什均衡。也许有人会说，如果两个囚徒事先定好了攻守同盟，可能就会出现（抵赖，抵赖）即（1，1）的结果。但是，在警察的严厉审问下，犯罪分子的心理防线最终都将被攻破。因为攻守同盟（即死不坦白）不构成纳什均衡，没有人有积极性遵守这个协定。因此，最终结果只能是作为纳什均衡的（坦白，坦白）即（15，15）。

实际上，“囚徒困境”是现实生活中许多现象的一个抽象概括，一旦陷入其中，要摆脱这个困境远非易事。例如，冷战时期两个超级大国长达40年的军备竞赛、各国的贸易保护主义倾向和寡头垄断企业之间的价格战都属于这种情况。

2.完全信息动态博弈——子博弈精炼纳什均衡

子博弈是指在给定条件下，从每一个行动选择开始至博弈结束又构成一个博弈，称为“子博弈”。子博弈又会进一步产生出更细的子博弈，或者我们暂且称之为“孙博弈”。无数的子博弈构成了一棵“博弈树”。在博弈论的著作中，一般把整个博弈也称为一个“子博弈”。下面我们来了解子博弈精炼纳什均衡。所谓子博弈精炼纳什均衡是指不包含不可置信威胁的纳什均衡。这里我们通过一个叫做“父子关系”的案例来说明。

案例5⁃2 父子关系

父亲与儿子关系一直很好，谁也离不开谁。然而，有一天，儿子突然迷上了网络游戏，经常不去学校上学，人也变得孤僻了，甚至有时彻夜不归。父亲忍无可忍，向儿子宣布：“如果你再不改过来，继续上网玩游戏的话，我将与你断绝父子关系。”这是父亲对儿子的威胁。从儿子方面来说，假定不考虑其他因素，面对父亲的威胁，他是否会就此罢手了呢？这要看父亲的威胁是否是可信的。如果父亲只是想吓唬吓唬儿子而已，那么父亲是不会与儿子断绝父子关系的。假如儿子也看清了这一点，那么，对于儿子来说。父亲的威胁就是不可置信的。结果是儿子排除了父亲不可置信的威胁，继续上网玩游戏。这个结果就是子博弈精炼纳什均衡。

3.不完全信息静态博弈——贝叶斯纳什均衡

贝叶斯（Bayes）是一位概率统计学家。贝叶斯纳什均衡，由海萨尼研究得出，它指的是这样一种类型依从战略组合：给定自己的类型和别人类型的概率分布的情况下，每一个参与人的期望效用达到了最大化，也就是说，没有人有积极性选择其他战略。我们通过案例4来分析这个问题。

案例5⁃3 市场进入阻挠

在某个行业领域，假设有一个垄断企业已在市场上，我们可称之为在位者，另一个企业想进入这个市场，我们可称之为进入者。在位者想保持自己的垄断地位，所以就要阻挠进入者进入。二者之间进行着博弈。在这个博弈中，进入者有两种战略可以选择：进入或不进入。在位者也有两种选择：默许或阻挠。对进入者来说，是否进入，取决于它对在位者的信息的掌握程度。假定进入者实际上并不完全了解在位者的信息，它只能依赖于对在位者类型的判断来做出决策。如果它判断在位者为高成本类型的概率为50%以上，那么它进入市场，在位者一般会选择默许，因为阻挠的成本或代价太高。所以，它就会做出进入的决策。而如果它判断在位者为低成本类型的概率为50%以上，那么它进入市场，在位者一般会选择阻挠，所以，它就会做出不进入的决策。这对它来说是最优战略。这个结果就是贝叶斯纳什均衡。

贝叶斯纳什均衡的一个重要应用领域是招标或拍卖方面。设想政府有一项大型建设工程要出包，选择要价最低的承包者。这时，不同投标者之间进行的就是一场博弈。假定每个投标者不知道其他投标者的真实生产成本而仅仅知道其概率分布，那么各投标者就要用概率分布方法来对对手进行判断。这时每个投标者在选择自己的报价时就面临着这样的交替：一方面，报价越低中标的可能性就越大；另一方面，给定中标的情况，报价越低利润就越小。博弈分析证明，每个投标人的标价依赖于它的类型，这里指的是生产成本，然而一般说来，贝叶斯均衡标价高于生产成本，二者之间的差异随着总投标者数量的增加而减少。这就是说，让更多的企业参加投标，对招标者是一件有利的事情。同样，政府在出卖或出租国有企业、国有土地时也是这种情形，只是这时，出价最高者中标。

4.不完全信息动态博弈——精炼贝叶斯纳什均衡

精炼贝叶斯纳什均衡是指当事人根据所观察到的他人的行为，利用贝叶斯规则来修正自己对他人类型的“信念”即修正主观概率，并由此选择自己的行动。这里所运用的贝叶斯规则是概率统计学中应用所观察到的现象修正先验概率的一种标准方法。例如，假设小周是小邓单位新来的一个同事，小邓对小周的人品并不了解，也就是说，小邓认为小周是好人或坏人的可能性相等，各自概率为0.5。一般认为，好人是不做坏事的。如果有一天小邓发现小周做了一件坏事，小邓就会修正自己对小周的看法，认为小周可能是坏人。这里，小邓事实上使用了贝叶斯规则，把他认为小周是坏人的概率由0.5修正为1。于是，小邓不想与小周在工作中共同合作。这个结果就是精炼贝叶斯纳什均衡。可见，当人们使用了贝叶斯规则修正先验概率以后，就要选择自己的行动。