资金时间价值计算中的注意事项

在2.2.2中我们讨论了资金时间价值计算的基本问题，即一次性收付款的终值和现值、年金的终值和现值，但是在现实的经济生活中，由于资金流量的不规则和时间分布的不统一，资金时间价值的计算变得复杂，因此我们除了要掌握简单资金时间价值的计算外，还需要掌握复杂资金时间价值的计算。

1.未知利率i的问题

未知利率的问题是在已知资金收付的规律、期数、年金、终值或现值等数据的基础上，利用终值或现值的计算公式，反推利率的数值。

例2-14　张先生欲承租一家店面，租期3年，店主要求现在一次性支付30 000元，张先生与店主协商能否有其他支付方式，店主考虑后提出其他两种付款方式。第一种：3年后一次性支付37 791元。第二种：每年年末支付12 000元。假设银行贷款利率为7%，银行小额贷款办理也很方便，请问张先生应该选择哪种支付方式？

张先生应该选择实际利率最低的方式。利率的计算方法有查表法和内插法两种。

（1）查表法。在复利计息方式下，查表法即通过计算出相关的终值系数和现值系数，在已知期数n的基础上，在相应的表格中反查出利率。

本题中，3年后一次性支付37 791元，相当于一次性收付款项业务，已知现值P=30 000，终值F=37 791，期数n=3，求i。

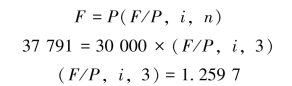
通过复利终值系数表，由n=3查得i=8%。

（2）内插法。当计算出的相关复利系数，在已知的期数基础上无法直接查得利率，就应该用内插法。内插法的公式为：

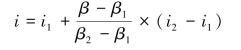
式中，所求的利率为i，i对应的现值或终值系数为β，β1和β2为现值或终值系数表中与β相邻的系数，i1和i2为β1和β2对应的利率数值，如表2-3所示。

表2-3　内插法分析表（一）

本题中，每年年末支付12 000元，即普通年金业务，已知A=12 000，P=30 000，求i。

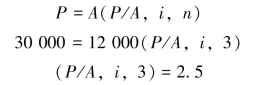
通过查年金现值系数表，当n=3，没有对应的利率，但是我们可以查得与（P/A，i，3）=2.5最接近的两个数值，如表2-4所示。

表2-4　内插法分析表（二）

即（P/A，9%，3）=2.531 3，（P/A，10%，3）=2.486 9。

通过内插法的计算公式可以求出实际利率。

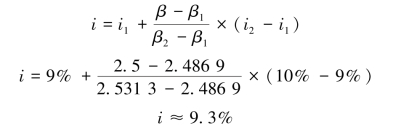
总结：不管是3年后一次性支付37 791元，还是每年年末支付12 000元，它们的实际利率均高于银行贷款利率7%，所以张先生应该从银行小额贷款30 000元，一次性支付3年的租金。

2.未知复利期限n的问题

未知复利期限n的问题与未知利率i的问题求解方法相似，区别在于此时利率i为已知，而期数n为未知。这类问题也有查表法和内插法两种计算方式。

（1）查表法。在复利计息方式下，查表法即通过计算出相关的终值系数和现值系数，在已知利率i的基础上，在相应的表格中反查出期数n。

例2-15　李先生现有存款80 000元，将其存入银行，当本利和累计为183 360元时再取出，作为养老基金，假设银行年存款利率为5%，问：李先生要存几年？

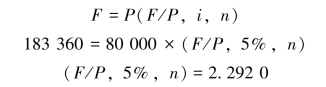
通过复利终值系数表，由i=5%查得n=17。

（2）内插法。当计算出的相关复利系数，在已知的利率基础上无法直接查得期数，就应该用内插法。内插法的公式为：

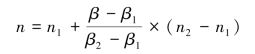
式中，所求的利率为i，i对应的现值或终值系数为β，β1和β2为现值或终值系数表中与β相邻的系数，i1和i2为β1和β2对应的利率数值，如表2-5所示。

表2-5　内插法分析表（三）

例2-16　郑某打算采用零存整取的方式准备一笔创业基金100万元，假设他每年扣除各种日常开销后可以存入银行8万元，银行存款年利率为5%，问郑某需要存多少年？

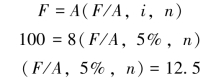
通过查年金终值系数表，当i=5%，没有对应的期数，但是我们可以查得与（F/A，5%，n）=12.5最接近的两个数值，如表2-6所示。

表2-6　内插法分析表（四）

通过内插法的计算公式可以求出复利期限。

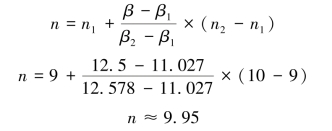
3.一年内多次计息的问题

我们在讨论复利计息时，给出的利率均为年利率，并都假设为每年复利一次，但实际上复利的计息期不一定总是一年，有可能是半年度、季度、月或日。比如某些债券半年计息一次，有的抵押贷款每月计息一次，而银行之间拆借资金均为每天计息一次。当利息在一年内要复利几次时，给出的年利率称为名义利率，只有每年复利一次的年利率才称为实际利率。遇到这种情况，我们可以采用以下两种方法计算求解资金的时间价值的问题。

（1）根据名义利率和实际利率的关系，将名义利率调整为实际利率。

因为：

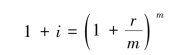
式中，i表示实际利率；r表示名义利率；m表示每年复利次数。

所以

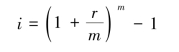
例2-17　某项目预计3年后获得本利和10 000万元，投资报酬率按8%计算，每半年复利一次，现在应投资多少元？（与例2-5对比）

根据题意，投资报酬率8%为名义利率，每年复利2次，根据公式可以求得实际利率为：

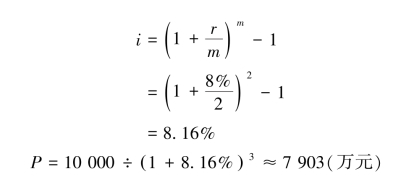
（2）不计算实际利率，而是调整有关指标，即将利率调整为，期数调整为m·n。根据这种方法，例2-17计算为：

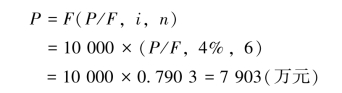
利息i=10 000-7 903=2 097（万元），比例2-5的利息2 062万元（10 000-7 938）多出35万元（2 097-2 062），原因就在于例2-17中的实际利率为8.16%，高于8%。

综上我们可以知道，当一年复利几次时，实际得到的利息要比按名义利率计算的利息高。

知识训练

一、判断题

1.资金时间价值相当于没有风险情况下的社会平均资金利润率。（　　）

2.利率不仅包含时间价值，而且包含风险价值和通货膨胀补偿率。（　　）

3.每半年付息一次的债券利息是一种年金的形式。（　　）

4.即付年金的现值系数是在普通年金的现值系数的基础上，系数+1、期数-1得到的。（　　）

5.递延年金有终值，终值的大小与递延期是有关的，在其他条件相同的情况下，递延期越长，则递延年金的终值越大。（　　）

6.已知（F/P，3%，6）=1.194 1，则可以计算出（P/A，3%，6）=3.47。（　　）

7.某人贷款5 000元，年利率是6%，每半年计息一次，则3年后该项贷款的本利和为5 955元。（　　）

二、不定项选择题

1.某人希望在5年后取得本利和20 000元，则在年利率为2%、单利计息的方式下，此人现在应当存入银行（　　）元。

A.18 114

B.18 181.82

C.18 004

D.18 000

2.某人目前向银行存入1 000元，银行存款年利率为2%，在复利计息的方式下，5年后此人可以从银行取出（　　）元。

A.1 100

B.1 104.1

C.1 204

D.1 106.1

3.某人进行一项投资，预计6年后会获得收益880元，在年利率为5%的情况下，这笔收益的现值为（　　）元。

A.4 466.62(www.xing528.com)

B.656.66

C.670.56

D.4 455.66

4.企业有一笔5年后到期的贷款，到期值是15 000元，假设存款年利率为3%，则企业为偿还借款建立的偿债基金为（　　）元。

A.2 825.34

B.3 275.32

C.3 225.23

D.2 845.34

5.某人分期购买一辆汽车，每年年末支付10 000元，分5次付清，假设年利率为5%，则该项分期付款相当于现在一次性支付（　　）元。

A.55 256

B.43 259

C.43 295

D.55 265

6.年金是指一定时期内每期等额收付的系列款项，下列各项中属于年金形式的是（　　）。

A.养老金

B.等额分期付款

C.融资租赁的租金

D.按照直线法计提的折旧

7.某企业进行一项投资，目前支付的投资额是10 000元，预计在未来6年内收回投资，在年利率是6%的情况下，为了使该项投资是合算的，那么企业每年至少应当收回（　　）元。

A.1 433.63

B.1 443.63

C.2 023.64

D.2 033.64

8.某一项年金前4年没有流入，后5年每年年初流入1 000元，则该项年金的递延期是（　　）年。

A.4

B.3

C.2

D.1

9.某人拟进行一项投资，希望进行该项投资后每半年都可以获得1 000元的收入，年收益率为10%，则目前的投资额应是（　　）元。

A.10 000

B.11 000

C.20 000

D.21 000

10.某项年金前3年没有流入，从第四年开始每年年末流入1 000元，共计4次，假设年利率为8%，则该递延年金现值的计算公式正确的是（　　）。

A.1 000×(P/A,8%,4)×(P/F,8%,4)

B.1 000×[(P/A,8%,8)-(P/A,8%,4)]

C.1 000×[(P/A,8%,7)-(P/A,8%,3)]

D.1 000×(F/A,8%,4)×(P/F,8%,7)

11.某人在第一年、第二年、第三年年初分别存入1 000元，年利率为2%，单利计息的情况下，在第三年年末此人可以取出（　　）元。

A.3 120

B.3 060.4

C.3 121.6

D.3 130

12.已知利率为10%的1期、2期、3期的复利现值系数分别是0.909 1、0.826 4、0.751 3，则可以判断利率为10%、3年期的年金现值系数为（　　）。

A.2.543 6

B.2.486 8

C.2.855

D.2.434 2

13.下列说法正确的是（　　）。

A.普通年金终值系数和偿债基金系数互为倒数

B.普通年金终值系数和普通年金现值系数互为倒数

C.复利终值系数和复利现值系数互为倒数

D.普通年金现值系数和资本回收系数互为倒数

14.某人于第一年年初向银行借款30 000元，预计在未来每年年末偿还借款6 000元，连续10年还清，则该项贷款的年利率为（　　）。

A.20%

B.14%

C.16.13%

D.15.13%

15.某人拟进行一项投资，投资额为1 000元，该项投资每半年可以给投资者带来20元的收益，则该项投资的年实际报酬率为（　　）。

A.4%

B.4.04%

C.6%

D.5%

16.某人决定在未来5年内每年年初存入银行1 000元（共存5次），年利率为2%，则在第五年年末能一次性取出的款项额计算正确的是（　　）。

A.1 000×(F/A,2%,5)

B.1 000×(F/A,2%,5)×(1+2%)

C.1 000×(F/A,2%,5)×(F/P,2%,1)

D.1 000×[(F/A,2%,6)-1]

三、计算题

1.某人决定分别在2002年、2003年、2004年和2005年各年的1月1日分别存入5 000元，利率为10%，每年复利一次，则2005年12月31日的余额是多少？

2.某公司拟租赁一间厂房，期限是10年，假设年利率是10%，出租方提出以下几种付款方案。

（1）立即付全部款项，共计20万元。

（2）从第4年开始每年年初付款4万元，至第10年年初结束。

（3）第1到8年每年年末支付3万元，第9年年末支付4万元，第10年年末支付5万元。

要求：通过计算比较该公司应选择哪一种付款方案。

3.某公司拟进行一项投资，目前有甲、乙两种方案可供选择。如果投资于甲方案，其原始投资额会比乙方案高60 000元，但每年可获得的收益比乙方案多10 000元。

假设该公司要求的最低报酬率为12%，方案的持续年限为n年，分析n处于不同取值范围时应当选择哪种方案。