资金时间价值的计算方法优化：

资金时间价值的计算方法与利息的计算方法相同，主要有单利和复利两种。

1.单利的计算

在单利的计算方法下，不管时间多长，每期的计息基础都仅是本金，之前产生的利息不加入本金重复计算以后的利息。

在计算中，经常使用以下符号：P——本金，又称期初金额或现值；I——利息；i——利率，通常指每期利息与本金之比；F——本金与利息之和，又称为终值；n——计算期数，通常以年为单位。

（1）单利利息的计算。公式如下：

例2-1　某人将10 000元存入银行，年利率为4%，按单利计算，5年后可获得多少利息？

知识卡片

一般在计算利息时，给出的利率均为年利率，当计息期不足1年时，以1年等于360天来折算。例如：某人2016年10月1日取得带息期票10 000元，年利率为9%，到2016年12月31日，利息为10 000×9%×[（31+30+31）÷360]=230（元）。

（2）单利终值的计算。单利终值是指一定量资金经过若干期后按单利计算的本利和。

当n=1~n时，可得：

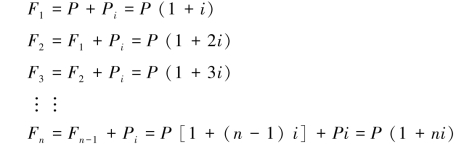
因此，单利终值的计算公式为：

例2-2　某人将10 000元存入银行，年利率为4%，按单利计算，5年后本利和为多少？

（3）单利现值的计算。单利现值是指未来某个时间点上一定量的资金（终值）按单利计算方式折合到现在的价值。单利现值的计算与终值的计算是互逆的，由终值折算成现值的过程称为折现。单利现值的计算公式为：

例2-3　某人希望在5年后获得12 000元的旅游基金，在利率为4%的情况下，按单利计算方式，此人现在需存入银行的本金为多少？

2.复利的计算

复利，俗称“利滚利”，即以利息生利息，在计算本期利息时，以本金加累计发生的利息之和为计息基础。

财务说说

拿破仑带给法兰西的尴尬

拿破仑1797年3月在卢森堡第一国立小学演讲时说了这样一番话：“为了答谢贵校对我，尤其是对我夫人约瑟芬的盛情款待，我不仅今天呈上一束玫瑰花，并且在未来的日子里，只要我们法兰西存在一天，每年的今天我将亲自派人送给贵校一束价值相等的玫瑰花，作为法兰西与卢森堡友谊的象征。”说完，拿破仑潇洒地把一束价值3个路易的玫瑰花送给该校的校长。

时过境迁，拿破仑穷于应付连绵的战争和此起彼伏的政治事件，把卢森堡的诺言忘得一干二净。可卢森堡对这位“欧洲巨人与卢森堡孩子亲切、和谐相处的一刻”念念不忘。1984年年底，卢森堡旧事重提，向法国提出违背“赠送玫瑰花”诺言的索赔：要么从1797年起，用3路易作为一束玫瑰花的本金，以5厘复利（即利滚利）计息全部清偿应付款项；要么法国政府在法国各大报刊上公开承认拿破仑是个言而无信的小人。

起初，法国政府准备不惜重金赎回拿破仑的声誉，却又被应付款项的数额惊呆了，原本3个路易的许诺，本息竟高达1 375 596法郎。经冥思苦想，法国政府斟字酌句给予答复：“以后，无论在精神上还是物质上，法国将始终不渝地对卢森堡大公国的中小学教育事业予以支持与赞助，来兑现我们的拿破仑将军那一诺千金的玫瑰花信誉。”这一措辞最终得到了卢森堡人民的谅解。

（1）一次性收付款项的终值与现值。

一次性收付款项是指在某一特定时点上一次性支出或收入，经过一段时间后再一次性收回或支出的款项。例如，现在将一笔10 000元的现金存入银行，5年后一次性取出本利和。

1）一次性收付款项终值的计算（已知现值P，求终值F）。

一次性收付款项的终值是指一定量的本金按复利计算若干期后的本利和。

当n=1~n时，可得：

因此，复利终值的计算公式为：

式中，（1+i）n被称为一次性收付款项终值系数，简称为“复利终值系数”，有时也被称为“1元的复利终值”，用符号（F/P，i，n）表示。例如，（F/P，8%，10）表示利率为8%、计息期为10期的复利终值系数。复利终值系数可以通过查阅复利终值系数表直接获得，复利终值系数表的第一行是利率i，第一列是计息期数n，相应的（1+i）n数值在交接处。通过查表可得（F/P，8%，10）=2.158 9。

复利终值的计算公式还可以表示为：

例2-4　某人将10 000元存放于银行，年利率4%，按复利计算，则5年后的本利和为多少？

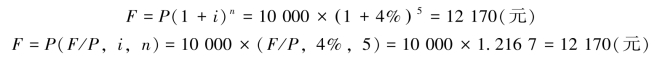
2）一次性收付款项现值的计算（已知终值F，求现值P）。

复利现值相当于原始本金，是指将来某一时点收到或付出的款项，按折现率i所计算的现在时点的价值。

由F=P（1+i）n=P（F/P，i，n）可得P=F÷（1+i）n=F÷（F/P，i，n），则复利现值的计算公式为：

式中，（1+i）-n称为一次性收付款项现值系数，简称“复利现值系数”，有时也被称为“1元的复利现值”，记作（P/F，i，n），可以查复利现值系数表获得。（P/F，i，n）和（F/P，i，n）互为倒数。

例2-5　某项目预计3年后获得本利和10 000万元，按投资报酬率8%计算，现在应投资多少元？

（2）年金的计算。

除了一次性收付款项外，在现实经济生活中，还存在一定时期内多次收付的款项，即系列收付款项，如果每次收付的金额相等，则这样的系列收付款项被称为年金。简而言之，年金是指一定时期内每次等额收付的系列款项，记作A。

年金的形式多种多样，保险费、养老金、折旧、租金、等额分期付款赊购和零存整取储蓄是等额付款年金；等额收款年金的形式有等额收款销售和整存零取储蓄等。

年金按照每次收付发生的时点和收付的次数可分为普通年金、预付年金、递延年金和永续年金。

1）普通年金。普通年金又称为后付年金，是指在一定时期内，从第一期起，每期期末等额发生的系列收付款项，如图2-1所示。

图2-1　n期普通年金

（a）普通年金终值的计算（已知年金A，求年金终值F）。

普通年金终值是指每期期末收付等额款项的复利终值之和。如果年金相当于零存整取储蓄存款的零存数，那么年金终值就是零存整取的整数，如图2-2所示。

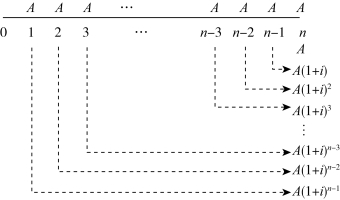
图2-2　n年普通年金终值分析

普通年金终值计算公式为：

两边同时乘以（1+i），则得到：

由式（2-2）-式（2-1），得：

所以，

式中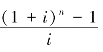，称作普通年金终值系数，简称“年金终值系数”，记作（F/A，i，n），它表示普通年金为1元、利率为i、经过n期的年金终值，可以通过查阅年金终值系数表得到有关数据。因此，年金终值的计算公式为：

例2-6　某人每月月末存入银行1 000元，年利率为4%，则1年后，该人可以得到的本利和为多少？

（b）年偿债基金的计算（已知普通年金终值F，求年金A）。

偿债基金是指为了在未来某个时点筹得一笔款项清偿债务或者投资项目而在每期期末分次等额存储的准备金。未来某个时点的款项就相当于年金终值，每期期末存储的偿债基金相当于年金。在复利计息的条件下，年偿债基金的计算相当于已知年金终值F求年金A，即年金终值的逆运算，其计算公式为：

式中，称作偿债基金系数，记为（A/F，i，n），与（F/A，i，n）互为倒数，可直接查阅年偿债基金系数表获得，也可通过年金终值系数的倒数推算出来。

年偿债基金m计算公式也可写作：

例2-7　假设某企业有一个3年后要投资的项目，估计需要200万元，若存款年利率为4%，则为了完成该投资项目，前3年每年年末需存入多少元？

（c）普通年金现值的计算（已知年金A，求年金现值P）。

普通年金现值是指一定时期内每期期末等额收付款项的复利现值之和，也就是为在每期期末取得等额收付款项，现在需要投入或借入的金额，如图2-3所示。

图2-3　n年普通年金现值分析(www.xing528.com)

普通年金现值的计算公式为：

上式通过等比数列求和的公式整理，可得：

式中，称作普通年金现值系数，简称为“年金现值系数”，记作（P/A，i，n），可以通过直接查阅年金现值系数表获得有关数值。普通年金现值的计算公式也可写作：

例2-8　某企业融资租入某设备，使用期限为10年，每年年末需要支付10 000元，年利率为4%，则租赁付款额的现值为多少？

P=A（P/A，i，n）=10 000×（P/A，4%，10）=10 000×8.110 9=81 109（元）

（d）年资本回收额的计算（已知普通年金现值P，求年金A）。

年资本回收额是在给定的时间内在每期末等额回收初始投入资本或清偿借款的价值指标。它相当于一次性投资每期期末等额获得的收益或者一次性借款每期期末等额偿还的款项。年资本回收额的计算是普通年金现值的逆运算，其计算公式为：

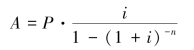
式中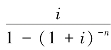，称作资本回收系数，记为（A/P，i，n），可直接查阅资本回收系数表或利用年金现值系数的倒数求得。年资本回收额的计算公式也可写作：

例2-9　某人从银行贷款30万元购买商品房，年利率6%，在10年内还清，每年年末需要偿还的金额为多少？

2）预付年金。

预付年金又称为即付年金或先付年金，是指在一定时期内每期期初等额收付的系列款项。它与普通年金的区别仅在于付款时间的不同，如图2-4所示。

图2-4　n期预付年金与n期普通年金对比

（a）预付年金终值的计算。

预付年金的终值是指各期收付款项的复利终值之和。

第一种计算方法：从图2-4可以看出，在期数n相同的条件下，预付年金与普通年金的付款次数相同，但由于其付款时间不同，预付年金终值要比普通年金终值多计算一期利息。因此，在n期普通年金终值的基础上乘以（1+i）就是预付年金的终值。其计算公式为：

第二种计算方法：由第一种方法推导而来。

因为F=A（F/A，i，n）（1+i），而（F/A，i，n）=，所以：

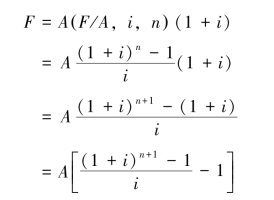
式中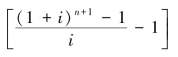，被称为预付年金终值系数，它是在普通年金终值系数的基础上期数加1、系数减1的结果，因此可以记作[（F/A，i，n+1）-1]。通过查阅年金终值系数表，得到（n+1）期普通年金的终值，然后再减去1，便可得到对应的n期的预付年金终值系数。因此，预付年金终值的公式也可以写作：

例2-10　某人决定连续10年，每年年初存入5万元作为养老基金，银行年利率为4%，则该人在第10年年末能一次取出的本利和为多少？

第一种方法：

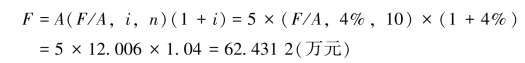
第二种方法：

（b）预付年金现值的计算。

预付年金的现值是指各期收付款项的复利现值之和。

第一种计算方法：从图2-4可以看出，在期数n相同的条件下，预付年金与普通年金的付款次数相同，但由于其付款时间不同，预付年金现值要比普通年金现值少折现一期。因此，在n期普通年金现值的基础上乘以（1+i）就是预付年金的现值。其计算公式为：

第二种方法：由第一种方法推导而来。

式中，被称为预付年金现值系数，它是在普通年金现值系数的基础上，期数减1、系数加1的结果，因此可以记作[（P/A，i，n-1）+1]。通过查阅年金现值系数表，得到（n-1）期普通年金的现值，然后再减去1，便可得到对应的n期的预付年金现值系数。因此，预付年金现值的公式也可以写作：

例2-11　某人分期付款购买数码商品，连续6期，每期期初支付款项5万元，年利率为6%，则该数码商品的现值为多少？

第一种方法：

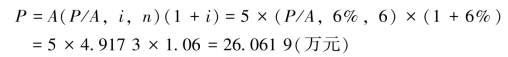
第二种方法：

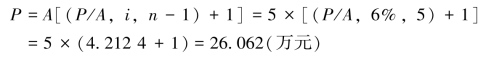
3）递延年金。

递延年金是指第一次收付款行为发生在第二期期末或若干期（假设为m）以后某期（假设为m+1）期末的系列等额收付款项。它是普通年金的特殊形式，它们都是发生在期末的系列等额收付款项。区分两者的唯一标准就是第一次收付款项是否发生在第一期期末，如果是，就是普通年金，如果不是，就是递延年金，如图2-5所示。

图2-5　递延年金与普通年金的对比

（a）递延年金终值的计算。

从图2-5可以看出，n期的递延年金在前m期期末没有发生年金的收付，从（m+1）期期末开始发生了共（n-m）期的年金收付，因此，递延年金的终值就是（n-m）期普通年金的终值，其计算公式为：

（b）递延年金现值的计算。

方法一：从图2-5可以看出，要计算递延年金的现值，可以先计算出n期普通年金的现值，然后减去前m期普通年金的现值，如图2-6所示。

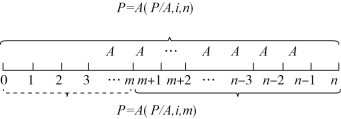
图2-6　递延年金计算分析（方法一）

其计算公式为：

方法二：从图2-6可以看出，n期的递延年金分成两部分，一部分为m期的递延期没有发生年金，另一部分为（n-m）期的普通年金期，因此我们可以现按照普通年金现值的计算方法先求出（n-m）期的普通年金现值，然后再把此现值按照复利现值的计算方法折现到第一期期初，即可求得n期递延年金的现值，如图2-7所示。

图2-7　递延年金计算分析（方法二）

第一步：P=A（P/A，i，n-m）。

第二步：P=F（P/F，i，m）。

其计算公式为：

例2-12　某投资项目于2016年年初开始动工，施工期3年，2019年年初投产，从投产日开始，每年年末可以获得收益20 000元，按复利率10%计算，则到2023年年末，该项目收益于2016年年初的现值为多少？

由题意得，n=8，m=3。

方法一：

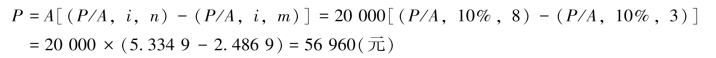
方法二：

4）永续年金。

永续年金是指无收付期限的系列等额款项，可视为普通年金的特殊形式，是一种期限趋于无穷的普通年金，如图2-8所示。

图2-8　n期（n→∞）永续年金

由于永续年金持续期无限，因此没法计算其终值，也就是说永续年金没有终值，但可以计算其现值，计算方法如下。

因为P=A（P/A，i，n）=A·，由于永续年金的期限n→∞，所以（1+i）-n→0，所以，永续年金现值的计算公式为：

例2-13　某人持有某公司优先股，每年每股股利为5元，如此人想长期持有该优先股，在利率为10%情况下，该股票的市价为多少？

这是一个求永续年金现值的问题，即假设该优先股每年股利固定且持续很长时间，计算出这些股利的现值之和，即为该股票的市价。