渠道和零售促销策略优化

11.4.1　考虑零售商促销的双渠道供应链应急决策与协调

在双渠道供应链中，考虑到制造商自己也有电子商务渠道，因此传统零售商需要面对更大的压力。为了对抗这种压力，一般来说零售商会使用促销活动。促销活动会吸引消费者，但是也会具有一定的费用。在突发事件存在的前提下，作为双渠道供应链，如何实现零售商促销的优化，也是一个重要课题。

在电子商务的发展中，越来越多的制造商使用自营的电商平台，或者通过其他网络平台进行销售，这挑战了以往传统中零售业寡头垄断的情况，因此就同时存在了电子渠道和零售渠道两种销售模式。电子渠道成了制造商转型的机会。而对于电子渠道的竞争，零售商使用了多种方式。这些努力有一定的效果，但是无可否认，双渠道并行而且合作，已经成了这个时代的主题。

在零售商促销方面的研究中，2012年，王素娟等人研究了国美和苏宁这两大零售业巨头，并提出在零售业中的促销以及贸易的供应链模型。在2014年，考虑到促销没有稳定的固定效果，张汉江设计了促销费用的分摊模型。2015年，慕银平等人对供应链中，折扣促销的决策和作用。2012年，李欣然设计了销量折扣契约，实现对VMI模式下零售商促销的系统协调。2014年，王胜东等人构建了一个在随机性需求的前提下，一个制造商以及两个零售商的广告协调策略，设计了最佳的广告投放量，并为两个竞争的零售商设计了利润共享契约。2015年，于爱民在联合促销而且具有随机需求的前提下，针对双渠道的供应链，研究了零售商和制造商之间的协调问题和价格竞争情况，他证明，回购契约对于双方来说都是有好处的，但是这不能够达成双渠道的协调。在2013年，张智勇等人基于微分对策，对分摊成本在渠道供应链广告合作方面的影响进行了研究。但是我们也需要看到，在这些文献中，突发事件带来的影响并没有纳入考量。所以，本次研究重点考虑零售商促销对传统渠道的影响，考察在成本和需求同时出现扰动的时候，双渠道供应链中的销售数量、促销投入以及价格决策，并对批发契约下的分散决策进行探讨。随后，设计出零售商出校增量价格折扣的协调分散供应链。

供应链中，假定存在一个零售商和一个制造商（同时拥有自身的电子销售渠道）。设定市场的总需求是a，电子渠道的需求比例是μ（0＜μ＜1），单位成本cm，电子渠道的零售价格是pd，零售商价格pr，渠道替代系数θ（0＜θ＜1），β代表的是通过零售商的广告和促销等增加的销售额。而促销成本则是一个关于传统渠道销量增加的二次函数ηβ2／2，假设η＞1／2（1-θ2）。

于是，就构建出了在促销情况下，零售商以及电子渠道的需求函数，如附录公式195。

可以得到供应链的利润如附录公式196。

∏（pd，pr，β）的海塞矩阵为负定矩阵，其顺序主子式为：｛-2，4（1-θ）2，-2［2η（1-θ2）-1］｝，因此是可微凹函数。

通过求解一阶条件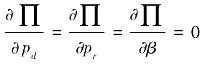，可以得到最优解如附录公式197。

所以，双渠道供应链的最优销售数量如附录公式198。

供应链最优利润如附录公式199。

综合考虑成本和需求搅动下的供应链的集中决策。如果供应链提供了短生命周期而且需要有准备期的产品，那么当制造商制订好了生产计划以后，遭遇突发事件引发市场规模和成本的改变。假定市场规模变化了Δa，成本变化了Δc，这种情况（当Δa＝0，Δc＝0时属于平稳状态）下有如下需求函数附录公式200。

供应链的总利润变为附录公式201。

其中（x）＋＝max（x，0）。

函数中第四项为增加产量带来的成本而第五项为减少产量带来的成本。

当的时候，供应链利润变成附录公式202。

当的时候，供应链利润变成附录公式203。

由于供应链利润均为零售价格的严格凹函数，因此可以求出最优的零售价格，存在三个情形。

如果制造商决定增加生产计划，这种决定的原因往往是由于突发事件引发的成本和需求扰动，导致供应链趋向于增加供应，而这种情况下，生产计划增加会导致单位成本提升。在某些时候，当企业认为外部市场具有替代品的时候，能够使用应急采购的方式提升供给量，但是不管如何决策，都会导致一定的成本。

这个时候，供应链的利润函数如附录公式204。

根据Kuhn-Tucker条件可以得到当：Δa≥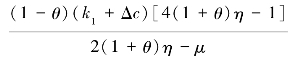的时候，

两个渠道市场售价如附录公式205。

传统渠道中零售商的努力程度如附录公式206。

两个渠道市场销量如附录公式207。

如果制造商决定减少生产计划，这种决定的原因往往是由于突发事件引发的成本和需求扰动，导致供应链趋向于减少需求，而这种情况下，供应商会减少生产，或者不减少生产而是以较低的价格在二级市场售出产品，但是不管如何决策，都会导致一定的成本。

这个时候，供应链的利润函数如附录公式208。

可以得到当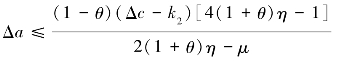：的时候，

两个渠道市场售价如附录公式209。

传统渠道中零售商的努力程度如附录公式210。

两个渠道市场销量如附录公式211。

如果制造商决定不变更生产计划：考虑到生产计划的变更，不管是增加产量还是减少产量都会带来成本，那么如果扰动较小，供应商就不会调整计划。

当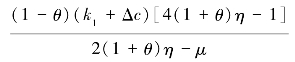的时候，

由于鲁棒性存在，因此，求解函数如附录公式212。

存在约束，可以求得附录公式213。

两个渠道市场售价为：

传统渠道中零售商的努力程度如附录公式214。

两个渠道市场销量如附录公式215和216。

得到结论11-7：如果双渠道供应链中同时存在成本和需求的扰动，那么计算得到最佳供应链决策。

电子渠道中，最佳零售价格如附录公式217。

传统渠道最优零售价格如附录公式218。

电子渠道销量如附录公式219。

传统渠道销量如附录公式220。

零售商促销努力的程度如附录公式221。

根据结论11-7：

①当的时候，制造商对渠道的供货重新规划，并增加生产计划。由于需求增加，传统渠道的销售努力提升，而由于生产成本提升，销售努力因此降低。此外，由于单位产量的成本增加，导致销售努力降低。

②的时候，制造商对渠道的供货重新规划，并减少生产计划。由于需求减少，传统渠道的销售努力降低，而由于生产成本降低，销售努力因此增加。此外，由于单位产量的成本降低，将会导致销售努力提升。

③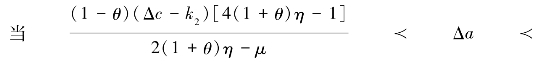的时候，制造商不对生产计划做出改变，而制造商和零售商之间所进行的销售额分配，将会对市场份额产生影响，但是不会改变总销量。在这里，成本的扰动不会干扰到销售努力程度，而传统的销售渠道中，销售努力的变动情况，取决于电子渠道的份额和扰动程度，如果电子渠道的份额更大，那么当需求增加的时候，努力程度降低。如果电子渠道份额较小，那么需求增加的时候努力程度也会提升。

④制造商在进行生产计划的变更的时候，其决策与渠道份额、替代系数、单位成本改变以及促销的投入相关。

11.4.2　考虑零售商双渠道供应链应急决策与协调

电子渠道的零售商建设双渠道供应链中一个独特的模式是，虽然制造商本身不直接面对消费者，而通过电子渠道可以与传统渠道面临同样的消费者，这种方式伴随着传统零售商的业务平台越来越强大，逐渐进入了我们的研究视野，当突发事件导致供应链在需求和生产成本出现扰动，如何协调零售商建立双渠道供应链已成为一个亟待解决的问题。

消费者越来越习惯于通过网络购买商品，制造商也在各种不同的平台或自建平台试图摆脱零售商的垄断，而传统的零售商也看到了电子渠道带来的商机，纷纷开始重新规划自己的商业模式，从经营的商店只有传统的线下转移到两线发展电子渠道，满足客户对电子渠道与传统渠道零售商的不同需求，于是就形成了双渠道供应链的模式。在双渠道供应链下模式的零售商发展非常迅速，例如Suning.com和苏宁实体店，国美在线和实体店，在内地市场中优衣库通过双渠道下沉实现销售暴增，这些都是经典的双渠道零售商案例。此外，双渠道零售商之间的专有的在线和离线渠道也形成了竞争与合作。

在从电商发展至新零售的今天，与电子渠道结合的零售巨头也充满了对于双渠道供应链零售模式的期待。天猫与银泰进行合作，实体店巨头沃尔玛收购一号店，阿里收购高鑫零售等线上线下企业深度融合，使双渠道供应链成为新零售企业的重要结构。

但是大多数学者在对电商供应链进行研究的时候，并没有太多涉及双渠道供应链结构的内容，更多的是双渠道作为传统供应链的补充形态。但是从集中决策的角度上，零售商双渠道、制造商双渠道、多零售商，这都是有着类似模型的。而在分散决策中，供应链就会有制造商双渠道中部不会表现出来的决策行为。对于零售商来说，传统渠道和电子渠道的冲突是必须得到解决的。此外在获得了双渠道优势之后，零售商原本的主导地位也会出现变化。如果有垄断零售商的存在，那么传统的以制造商为主导的Stackelberg博弈也就无法反映出真实情况。在2011年，肖剑等人考虑到供应链中具有渠道冲突，所以在电子渠道中的一些订单就被转交给零售商。这本质上，也是在运行中的零售商双渠道供应链。此外，他们还研究了制造商与零售商的合作模型。在2013年，张辉等人基于收益共享契约，在零售商的双渠道方面，对三种不同的收益共享契约的协调情况进行了验证。但是目前还没有研究过突发事件在零售商双渠道方面导致的决策和协调问题。在这个部分，针对一个零售商和一个制造商构成的零售商双渠道供应链，研究了由于突发事件，引发成本和需求同时扰动的运营决策问题，并给出了最佳的渠道价格、产量以及利润，并对不同范围的扰动信息价值进行分析，对这种情况设计了契约进行协调。

在双阶段供应链中，有一个零售商和一个制造商。该供应链的产品是生命周期较短，而且需要一定的生产周期的产品。在本节的研究中，认为零售商具有传统渠道和电子渠道。这个时候市场需求为a，电子渠道需求比例μ（0＜μ＜1），成本为cm，电子渠道价格为pe，传统渠道价格为pt，两个渠道具有一定的价格竞争关系，替代系数为θ（0＜θ＜1）。因此，就构筑出两个渠道的需求函数，如附录公式222。

因此，可以得到供应链的最优利润如附录公式223。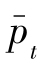（，）∈arg max∏（pe，pt）。

∏（pe，pt）是关于（pe，pt）的严格可微凹函数。

因此，可以得到双渠道供应链的最优零售价格如附录公式224。

渠道销售数量如附录公式225。

制造商的产量如附录公式226。

双渠道供应链利润如附录公式227。

在成本和需求出现扰动的情况下，对双渠道供应链均衡进行考虑。有很多突发事件都是在短时间内发生而且引发巨大的影响。另外，法律变化以及技术进步等情况，都会影响到供应链，产生扰动。假定由于突发事件，成本和市场出现变化。市场的变化量为Δa，成本的变化量为Δc。

这个时候，零售商的电子渠道销量如附录公式228。

零售商的传统渠道销量如附录公式229。

整体上，生产数有如下变化：。假定制造商在增加以及减少产量的时候，需要单位成本k1，k2（0＜k1，k2＜cm）。

因此在双因素扰动下的双渠道供应链利润函数如附录公式230。

其中：（x）＋＝max（x，0）。

在函数中，第三项是增加产量的成本，第四项是减少产量的成本。

如果不减少生产计划：

当

供应链利润函数变成附录公式231。

可以求出最优的渠道零售价格。

根据Kuhn-Tucker条件，求解函数如附录公式232。

可以得到两种情形：

情形1：若λ＝0，则当Δa≥2（1-θ）（Δc＋k1）的时候，

两个渠道市场售价如附录公式233。

两个渠道市场销量如附录公式234。

情形2：若λ＞0，则当Δa＜2（1-θ）（Δc＋k1）的时候，

两个渠道市场售价如附录公式235。

两个渠道市场销量如附录公式236和237。

因此，情形2下制造商的生产计划不变。

考虑不增加生产计划的情形：

当＋≤＋的时候，

供应链利润函数变成附录公式238。

根据Kuhn-Tucker条件，求解附录公式239。

同样也存在两种情形：

情形3：若λ＝0，计算同情形2，得到当Δa≥2（1-θ）（Δc-k2）的时候，

两个渠道市场售价如附录公式240。

两个渠道市场销量如附录公式241和242。

情形4：当λ＝0，则当Δa≤2（1-θ）（Δc-k2）的时候，(www.xing528.com)

两个渠道市场售价如附录公式243。

两个渠道市场销量如附录公式244。

结论11-8：双渠道供应链集中决策，面临需求和生产成本同时扰动的时候，供应链存在最优决策。最优电子渠道销售价格如附录公式245。

最优传统渠道价格如附录公式246。

最优生产数量如附录公式247。

定义直线Δa＝2（1-θ）（Δc＋k1）和直线Δa＝2（1-θ）（Δc-k2），如下图，就能够得到制造商的生产计划的决策区域。如果扰动位于区域D1的时候，制造商增产；当扰动位于区域D2的时候，制造商减少生产；当扰动范围处于区域D3的时候，产量不变。

图11-2　扰动发生后零售商双渠道集中决策区域

进一步对在双渠道供应链中，零售商对扰动应对的价值当突发事件扰动成本和需求，在零售商双渠道供应链下进行一体化的最优化决策，总利润如附录公式248。

其中，

在对原策略进行计算的时候，大部分研究者对价格决策参数进行考虑（，），但是产量会随着向量产生变化，在发生扰动之后，必须要发现扰动，才能调整产量。所以在原来的策略中，制造商不会变更产量。在本书中，原策略模型的决策参数是（，，），于是决策范围被分成六个区域。

供应链产品是有周期性的短生命产品，原策略无法及时调整计划，于是就会出现产能的过剩或不足。但是临时采购以及打折处理将会带来更高的单位成本。为了便于计算，假定不能直接购买产品，而过剩产品没有残值。那么，发生扰动之后，使用原策略的时候，供应链的利润函数如附录公式249。

其中，［x∧y］＝min（x，y）。

在扰动发生后，行动价值归纳如下表。

图11-3　扰动发生后沿用原策略决策区域

表11-1　双渠道供应链扰动信息的价值

继续对成本和需求同步扰动前提下的双渠道供应链考虑。作为供应链中最容易实现的契约，在双渠道供应链中，各种渠道广泛使用这个契约。在零售商双渠道的供应链中，博弈由制造商主导，其能够先给出批发价格w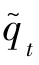（，），随后根据批发价，零售商制定零售价和电子渠道售价。

在扰动发生之后，零售商和制造商利润如附录公式250和251。

结论11-9：在双渠道供应链的分散决策下，零售商和制造商存在Stackelberg博弈，当供应链面临需求和成本的扰动，那么就采用数量折扣契约达成供应链协调，契约参数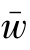（，η）满足附录公式252。

关于策略参数，制造商和零售商具有如下的利润函数附录公式253—254。

证明：

求解方程如附录公式255。

可以得到零售商双渠道售价关于契约参数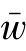（，η）的反应函数如附录公式256。

当Δa≥2（1-θ）（Δc＋k1）的时候，若附录公式257，则附录公式258成立。

当2（1-θ）（Δc-k2）＜Δa＜2（1-θ）（Δc＋k1）的时候，若附录公式259，则附录公式260成立。

当Δa≤2（1-θ）（Δc-k2）的时候，若附录公式261，则附录公式262成立。

证毕。

根据上面的结论可以发现，零售商双渠道的供应链，在数量折扣契约w（，），的情况下，能够实现协调，契约参数（，η）的策略组合为无穷多个，所以认为该契约具备抗突发事件能力。另外如果零售商双渠道供应链处于平稳状态（Δa＝Δc＝0），通过数量折扣契约如附录公式263，可以实现对平稳状态下零售商双渠道供应链的协调，而基本模型决策的结果与渠道定价的决策参数相同。

随着建设电子渠道和零售商零售渠道，双渠道模式的逐步成熟，这一段的突发事件造成需求和生产成本扰动的零售商在双渠道供应链的决策与协调策略，计算不同的扰动情况下的供应链渠道的零售价格、批发价格、数量、生产和供应链的最优利润。对扰动发生后的主要策略执行的决策进行了划分和计算，在不同干扰、设计协调需求和生产成本中断的零售商的双渠道供应链的价值。

11.4.3　强势零售商双渠道供应链应急决策与协调

在零售业中，强势零售商一种常见的商业个体。其中，国内强势零售商的典型代表就是国美和苏宁。而在国际上，典型的强势零售商就是家乐福和沃尔玛。此外，在电子商务领域，京东和天猫就是强势零售商。现在，传统强势零售商已经开始重视并着手双渠道建设，强势零售商在双渠道供应链中的决策以及协调，已经成了新的研究视角。在这一节中，针对供应链博弈，基于零售商为主导的Stackelberg博弈，对双渠道供应链的应激协调策略研究，并设计定价契约实现协调。

传统的供应链研究，一般制造商被假定为博弈的主导方。一方面，这是考虑到了供应链会涉及上游的生产和采购；另一方面，传统供应链的立足点一般是制造商。而从20世纪以来，零售业的聚集趋势越来越明显。在超市领域，众多超市在一定的区域占领一定的规模，这样也就能够在于供应商的较量中，获得主导地位。在商场品牌里，注入新世界、王府井等也有一定的主导地位。此外在电商行业里，天猫京东等，也都耳熟能详。这些商家发现了电子商务的大发展，并且主动出击，主导了渠道的建设。通过并购或者自己开拓电子商务渠道，强大的零售商现在有了越来越明显的双渠道战略。

在供应链中，强势零售商是具有主导地位的，所以这样的供应链与传统的供应链有很大的不同，对此学者也有一定的而研究。Choi是比较早的以定量方式研究以零售商为主导的供应链的学者之一，他构建了以零售商为主导的供应链价格模型。我国学者刘志学等人，对于一个供应商以及一个零售商的供应链进行了分析，通过对其收入共享契约的研究，说明了在供应链中，主导权的作用。此外还有人研究了短生命周期产品在以零售商为主导的双渠道供应链中的订货策略，并且基于某个大型商场的数据，实现了数值分析。

目前在这方面的研究文献还不是很多，具体到针对以零售商为主导的双渠道供应链的研究就更少。现在，苏宁等强势供应商越来越多地进入到双渠道中，所以在这一章，试图构建一个基于强势零售商的双渠道供应链模型，并且分析在成本和需求同时产生扰动的时候，批发价格契约的供应链应急决策，并且设计了两个定价契约，实现对成本与需求同时扰动情况下的，基于强势零售商双渠道供应链的协调。

一个两阶段的供应链，其中有零售商和制造商各一个。供应链的产品是生命周期短而且需要一定生产周期的产品，零售商具有双渠道且是博弈的主导方。假设需求a，电子渠道比例为μ（0＜μ＜1），单位成本为cm，电子渠道价格为pe，传统渠道价格为pt，电子渠道和传统渠道中价格替代系数为θ（0＜θ＜1）。构建供应链中电子渠道和传统渠道面临的需求函数如附录公式264。

因此，可以得到供应链的最优利润如附录公式265。

∏（pe，pt）是关于（pe，pt）的严格可微凹函数。

因此，可以得到双渠道供应链的最优零售价格如附录公式266。

双渠道销售数量如附录公式267。

制造商的产量如附录公式268。

双渠道供应链利润如附录公式269。

先考虑在成本和需求都出现扰动的情况下，强势零售商的分散决策。在集中决策中，没有博弈关系，因此参照结论，双渠道零售商在集中决策的时候，针对扰动有最佳决策。

最佳的电子渠道价格如附录公式270。

最优传统渠道价格如附录公式271。

最优生产数量如附录公式272。

基于主从博弈的原理，参照Choi提出的零售商主导的模型，基于市场需求，零售商先给出边际利润，而制造商基于生产成本，设定批发价。零售商售价如下：

其中mi（i＝e，t）为零售商的电子渠道与传统渠道的单位边际利润。

假设需求和生产成本同时扰动下零售商的零售价格如附录公式273。

这个时候，零售商的利润函数如附录公式274。

制造商利润函数如附录公式275。

求解，得到：

当的时候，制造商的批发价格对零售商双渠道单位边际利润（i＝e，t）的反应函数如附录公式276。

因此，求解可以得到平稳状态下零售商的决策值：

零售商的电子渠道和传统渠道的边际利润如附录公式277。

制造商的批发价格如附录公式278。

这个时候，零售商利润如附录公式279。

制造商利润如附录公式280。

当的时候，制造商的批发价格对零售商双渠道单位边际利润（i＝e，t）的反应函数如附录公式281。

因此，求解可以得到平稳状态下零售商的决策值：

零售商的电子渠道和传统渠道的边际利润如附录公式282。

制造商的批发价格如附录公式283。

这个时候，零售商利润如附录公式284。

制造商利润如附录公式285。

从以上可以看出，，所以如果有较大的扰动，批发价格契约就不能实现以零售商为主导的，供应链协调。

当的时候，制造商批发价对于零售商边际利润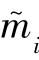（i＝e，t）的反应函数如附录公式286。

对其进行求解，可以得到在平稳情况下，零售商的决策。

在电子和传统渠道零售商边际利润如附录公式287。

批发价格如附录公式288。

这个时候，零售利润如附录公式289。

制造商利润如附录公式290。

从以上可以看出，，所以在具有较小扰动的情况下，批发价格契约能够帮助实现供应链的协调。

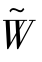所以在分散决策下，作为博弈的主导方，强势零售商的行为会有一定的变化。如果成本和需求同时扰动，假定在扰动之后，零售商会针对传统渠道对制造商收取以及就电子渠道收取的渠道许可费，制造商则是以的价格批发给零售商，零售商有边际利润（i＝e，t），这个时候，

零售商的利润函数如附录公式291。

制造商利润函数如附录公式292。

求解，在需求和生产成本同时扰动状态的时候，供应链具有以下三个情形。

情形1：当Δa≥2（1-θ）（Δc＋k1）的时候，制造商批发价针对零售商的单位边际利润函数如附录公式293。

联立，得到了对于零售商来说最优的边际利润参数如附录公式294。

这个时候，零售商利润如附录公式295。

制造商的利润如附录公式296。

这个时候

要实现最优化的供应链Pareto，就需要确保在两个定价契约之下，供应链双方都有大于批发价格契约的利润。这时候，联立方程，求得一次性转移支付的参数值，由于转移支付的范围表述比较繁琐，所以在算例中间以数值的形式描述。

情形2：当2（1-θ）（Δc-k2）＜Δa＜2（1-θ）（Δc＋k1）的时候，

联立方程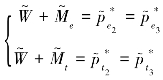，能够得到最优化的零售商边际利润参数如附录公式297。

情形3：Δa≤2（1-θ）（Δc-k2）的时候，

制造商的批发价格对零售商双渠道单位边际利润（i＝e，i）的反应函数如附录公式298。

联立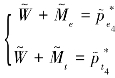，可以得到零售商最优的边际利润参数如附录公式299。

我们可以从中发现，零售商边际利润与调整成本无关，因为生产计划已经确定，因为零售商的供应链的主导方，制造商是弱势一方的供应链博弈，制造商将承担这部分损失。

现在苏宁、国美、沃尔玛和其他零售商电子渠道都在建设中或已经完成建设，作为强势零售商主导的供应链端的双渠道模式已经成为我们研究的重点，本章研究了突发事件引发的需求和生产成本扰动的情况下，强势零售商在双渠道供应链的决策与协调策略，通过对不同扰动状况下双渠道供应链零售商分散决策的情况进行计算，得到了批发价格契约和两合同定价的决策值，批发价格契约在干扰范围小（鲁棒区域）的时候可以实现双渠道供应链零售商的协调，但是在干扰范围非常大的时候，批发价格合同不能协调供应链。然后本章设计了两个零售商定价契约协调需求和生产成本中断的双渠道供应链。