风险型决策方法,一般先预计在未来实施过程中可能出现的各种自然状态(即情况),如市场销售状况可能有好、中、坏三种,估计这三种状态可能出现的概率。然后,根据决策目的提出各种决策方案,并按每个方案计算出在不同的自然状态下的损益值,称为条件损益。最后,按下式计算出每个方案的损益期望值,进行比较,择优选用:
EVMj=ΣPiQij
式中:EVMj——第j个方案的损益期望值,j=1,2,3,…,n;
Pi——第i种自然状态出现的概率,i=1,2,3,…,n;
Qij——第j个方案在i种自然状态下的条件损益值。
风险型决策方法的种类,主要有下列两种:
(一)决策表法
决策表法是利用决策矩阵表(又称期望值表),计算各方案的损益期望值进行比较的一种方法。
兹举例说明决策表法的运用如下:例如,设某厂进行生产能力决策。根据市场预测可能有好、中、差三种自然状态,市场形势好,年销售量可达10万件,市场形势中等时,年销售量8万件,市场形势差时,只能销售5万件,其概率分别为0.3、0.5、0.2。与之相对应,生产能力可有年产10万件、8万件、5万件三种方案。年产10万件时,单件成本为6元,但如果卖不出去,则未卖出的产品就积压报废,其成本由已销产品承担。年产8万件时,单件成本为7元。年产5万件时,因规模更小,成本增大,每件为8元。每件单价预计为10元。现计算其条件损益及进行决策如下:
方案Ⅰ:年产10万件,其条件损益为:
在销售好时:10×10-10×6=40(万元)
在销售中等时:8×10-10×6=20(万元)
在销售差时:5×10-10×6=-10(万元)
方案Ⅱ:年产8万件,其条件损益为:
在销售好和中等时:8×10-8×7=24(万元)
在销售差时:5×10-8×7=-6(万元)
方案Ⅲ:年产5万件,不论销售好、中、差,均只能销出5万件,
其条件损益为:5×10-5×8=10(万元)
现列出决策矩阵表,如表5-2所示。
表5-2 生产能力决策矩阵表
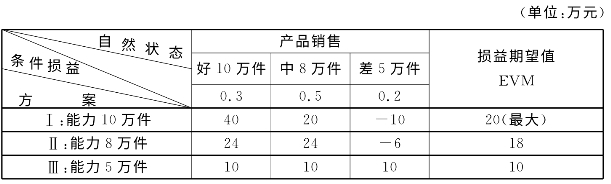
各方案的期望值计算如下:
方案Ⅰ:EVM1=(0.3×40)+(0.5×20)+0.2×(-10)=20(万元)
方案Ⅱ:EVM2=(0.3×24)+(0.5×24)+0.2×(-6)=18(万元)
方案Ⅲ:EVM3=(0.3×10)+(0.5×10)+(0.2×10)=10(万元)
由表5-2可知,方案Ⅰ的期望值为20万元,最大,应该选择方案Ⅰ。
(二)决策树法
决策树法是利用树枝状图形列出决策方案、自然状态、自然状态概率及其条件损益,然后计算各个方案的期望损益值,进行比较选择。其原理与决策表法相同,但能形象地分析决策的过程,并能解决较复杂的多级决策问题。(https://www.xing528.com)
决策树图形由决策点、方案枝、自然状态点和概率枝组成,如图5-1所示。
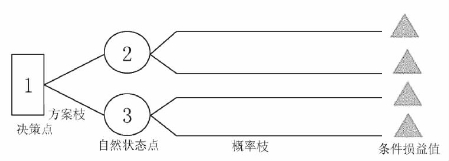
图5-1 决策树
其决策步骤如下:
第一步:绘制决策图。首先由决策点开始,用符号表示,自左至右展开,从决策点引出方案枝,有多少方案就有多少分枝。然后,在方案枝后面接上自然状态点,用“○”表示。从自然状态点引申出可能遇到的自然状态,称为概率枝,把可能出现的概率写在上方。如此顺序进行(如果是多级决策),直至最后的概率枝为止。最后,在最终的概率枝末端写上它的条件损益值。
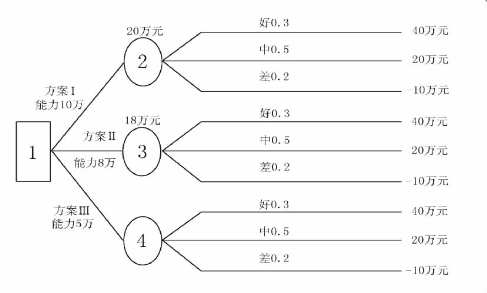
图5-2 单级决策示意图
第二步:计算期望值。从右往左按逆向顺序进行计算,把结果填在自然状态点上。在期望值计算时,如果有投资额,则应减去投资额,并将投资额写在方案枝下方。
第三步:比较不同方案的期望值,选出合理决策方案。保留期望值大的方案,未被选用的方案用两条平行短线截断,称为剪枝。以上例用决策树法进行决策,如图5-2所示。
其结果与上述决策表法相同。
上例为单级决策,如果是多级决策(序贯决策),则决策表法难以解决,而必须采用决策树法。
利用决策树法进行多级决策的方法举例如下。
例如:设生产销售某一新产品,根据市场预测,该产品的销路好的概率为0.7,销售差的概率为0.3。某企业为了生产该产品有两个方案。甲方案是建大厂,投资200万元,可使用10年,如销路好,每年可获利70万元(未计入投资费,下同);若销路差,每年亏损15万元。乙方案分两步走,先建小厂,只投资100万元,也可使用10年,如销路好,每年获利32万元;销路差,每年仍可获利10万元。若2年后证明销路好,则扩建为大厂,追加投资130万元,使用8年,每年可获利60 万元。若证明销路差则不扩建。这是一个多级决策问题,绘制成决策树如图5-3所示。
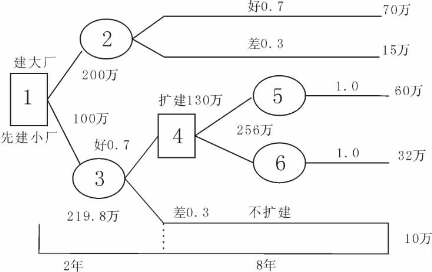
图5-3 多级决策示意图
计算各自然状态点的期望值如下:
点2:[(0.7×70)×10+0.3×(-15)×10]-200=245(万元)
点5:(1×60)×8-130=350(万元)
点6:(1×32)×8=256(万元)
点3:[(0.7×32)×2+(0.7×350)+(0.3×10)×10]-100=219.8(万元)
从计算结果可以看出,还是建大厂较好。
风险型决策主要受估计的概率影响,概率不准或发生变化,其结果则不同,会引起失误。为了验证决策方案选择的可靠性,要测定一下概率变化的幅度对决策方案选择的影响。这需要计算出一个临界概率进行分临界概率是使两个方案的期望值相等时的概率,如果达到这个概率,则两个方案的效果相同。以上例数据说明临界概率的求法如下:
设销路好的概率为P,则销路不好的概率为(1-P)。两个方案的期望值相等时,其恒等式如下:
[(P×70)×10+(1-P)×(-15)×10]—200
=[(P×32)×2+(P×350)+(1-P)×10×10]-100
整理后得:
P=0.653
即销路好的概率只要大于0.653,则该项决策(取建大厂的决策)仍然可靠。如果销路好的概率低于0.653,则该项决策就要相应改变,改为先建小厂的方案。目前估计销路好的概率为0.7,与临界概率相差0.047,即4.7%左右,决策的可靠性稍强。反之,若现行估计的概率与临界概率很接近,则可靠性差。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




