使用仿射密码对文件进行加解密

【任务描述】

已知仿射密码的密文为“JACKOZOO”，字母表为Z26，密钥K＝（11，7），试使用手工计算和CAP 4软件两种方法进行解密。

【任务分析】

仿射密码和移位密码一样，也是一种置换密码。不同的是，移位密码使用的是模n加，而仿射密码使用的是模n乘。在安全性方面，仿射密码同移位密码一样，也是较差的，这两种密码都没有隐藏明文的字频信息，破解者能够轻易实现破解。

把加法密码和乘法密码联合起来，就得到了所谓的仿射密码。仿射密码有两个密钥，乘法密码使用第一个密钥，加法密码使用第二个密钥。

【知识准备】

1.仿射变换

仿射密码是一种置换密码。加法密码和乘法密码结合就构成仿射密码。仿射变换就是“线性变换”＋“平移”。线性变换是通过矩阵乘法来实现的，仿射变换则是通过矩阵乘法和矩阵加法实现的。

仿射变换可以写成Y＝AX＋b的形式。线性变换不能表示平移，而仿射变换则可以，仿射变换在几何学上相当于两次平移变换与一次原点旋转变换，如图3-21所示。

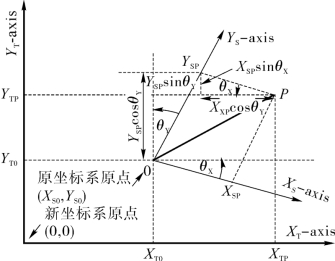
图3-21　仿射变换的几何学含义

2.模逆

模就是取余，在现代公钥密码体制中，加密和解密的过程都涉及求解模逆元的问题。求解模逆元，可以使用穷举法和扩展欧几里德算法等多种方法。

1）扩展欧几里德算法

扩展欧几里德算法是计算最大公约数的一个方便实用的方法。

将123和11都表示成x×123＋y×11的格式，然后相减，在最右侧一栏写上每次减去的被减数的倍数，依次进行，直到减数变为1为止。然后取第三列的最下面的一个数，再对123取模，即得11对123的模逆。

该算法的好处是以该算法的程序求任何模逆都是非常高效的。为了加深理解，看如下例子：

求1 211对13 211的模逆。

2）求解过程

若a，b两数的乘积对正整数n取模的结果为1，则称a，b互为对方的模逆。若a，b互为n的模逆，即b为a的模n的逆元，则b为a-1mod n，记为a-1 b≡1 mod n。

只有当a与n互素的时候，a才是有模逆的。在其他情况下是不存在模逆的，比如2对26就没有模逆。

思考：如何求11对123的模逆？

【任务实施】

1.仿射密码的加密原理介绍

1）移位密码的加密原理

移位密码也称为加法密码，移位密码的加密过程实际就是密钥的加法。其加密函数表示如下：

yi＝xi＋k mod 26

明文是xi，密钥是k，将明文加上密钥的取余部分，就得到了密文yi。

2）仿射密码的加密原理

（1）在仿射密码加密中，字母表中的字母被赋予一个数字，例如，a＝0，b＝1，c＝2，…，z＝25。

仿射密码加密的密钥为0～25的数字对（a，b）。a与26的最大公约数必须为1，这就是说能整除a和26的数只有1。现在假设m为明文字母的数字，而c为密文字母的数字，那么，这两个数字有如下关系：

c＝(am＋b)mod 26

m＝a-1(c-b)mod 26

其中，mod 26的操作是除以26，得其余数。

（2）仿射密码用到的仿射函数表示为

e（x）＝ax＋b mod 26，且a与26的最大公因子为1，密钥就是（a，b）。

仿射密码加密的思路为：首先将明文乘以密钥的一部分，然后再加上密钥的剩余部分。

在上述仿射函数中，x代表明文，先将明文乘以密钥的一部分a，然后再加上密钥的剩余部分b mod 26，求解得到密文e（x）。

仿射密码的密钥空间仅比移位密码的大一些，密钥空间＝（a可以取的值）×（b可以取的值）＝12×26＝312。此外，仿射密码拥有与移位密码同样的缺点，即明文和密文之间的映射关系是固定的。因此，使用频率分析方法一样可以轻而易举地破解仿射密码。

2.仿射密码加解密实例

例3.4　已知加密使用了仿射密码，密文为“JACKOZOO”，使用模逆运算进行破解。

解：　将26个字母与0～25的整数建立一一对应关系，其字母的表值具体如表3-4所示。

表3-4　例3.4字母的表值

（1）求11对26的模逆：

11-1mod 26＝19

（2）解密变换为：x＝19（y-7）mod 26

（3）由JACKOZOO

所以明文为“MXJFDEDD”。

例3.5　使用仿射密码解密密文“AXG”，密钥k＝（7，3）。

解：　（1）3个字母对应的数值是0、23、6。

（2）解密过程如下：

由Dk（c）＝k3（c-k2）mod n（其中（k3×k1）mod 26＝1）；

可知k3×7＝1（mod 26）（其实，就是1/mod 26），也就是存在整数t，使

利用辗转相除法求解k3：

(www.xing528.com)

（对26作形如a×b＋c的分解，其中c是余数）

（对7作形如a＝c×m＋n的分解，其中a，c是上一步的，m是乘数，n是余数）

（一直循环上一步，直到余数n＝1）

进行回代：

1＝5-2×2

＝5-（7-5×1）×2（第一个2用式（3-6）代替，也就是2＝7-5×1）

＝3×5-2×7

＝3×（26-7×3）-2×7（5用式（3-5）代替，也就是5＝26-7×3）

＝-11×7＋3×26（直到不用进行代替，也就是得到只有7和26的表达式）

对比式（3-4）可知：

t＝3，k3＝-11

所以：

Dk(c)＝k3(c-k2)mod n＜＝＞Dk(c)＝-11(c-3)mod 26

对于第一位A：

-11(0-3)mod 26＝(-11×-3)mod 26＝7

对于第二位X：

-11(23-3)mod 26＝(-11×20)mod 26＝(-220)mod 26＝(26×-9)＋14＝14

（使用计算器求（-220）mod 26，不同的计算器会有不同的结果，百度的计算器求得是14，不能直接在计算器上输入“-220mod 26”，那样会得出负数）

其实，可以算出（-11）mod 26＝15，再计算（15×20）mod 26＝14。

对于第三位G：

-11（6-3）mod 26＝（-11×3）mod 26＝（-33）mod 26＝19（计算方法同上）

三个明文值为7，14，19，对应的明文是HOT，也就是hot。

3.仿射密码的加解密算法

仿射密码的加解密算法是：

C＝Ek(m)＝(k1m＋k2)mod n

其中，C是密文；k1、k2是密钥；E是加解密方法；m是明文。

M＝Dk(c)＝k1(c-k2)mod n

仿射密码具有可逆性的条件是gcd（k，n）＝1。

当k1＝1时，仿射密码变为加法密码：当k2＝0时，仿射密码变为乘法密码。

仿射密码中的密钥空间的大小为nφ（n），当n＝26时，φ（n）＝12，因此仿射密码的密钥空间为12×26＝312。

仿射密码的加密流程如图3-22所示。

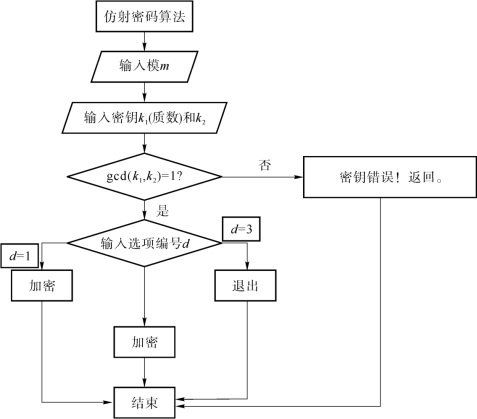
图3-22　仿射密码的加密流程图

4.使用CAP4软件进行仿射密码加解密

1）使用CAP4软件进行加密

步骤1：在CAP4软件中加载要加密的明文“mw.txt”。

步骤2：选择“Cipher”→“Affine Cipher”选项，弹出图3-23所示对话框。

图3-23　设置加密密钥

步骤3：选择“Affine Cipher”→“Encipher”选项进行加密，如图3-24所示。

图3-24　进行加密

2）使用CAP4软件进行解密

解密的前提是已经知道密文是采用仿射密码加密的。

步骤1：打开CAP4软件，加载已经获取的密文“fsbhmi.txt”，并单击“Basic Tools”工具条中的“Freq”按钮，统计密文中每个字母出现的频率，如图3-25所示。

图3-25　统计密文中字母出现的频率

通过统计可知，密文中出现频率最高的字母依次是X、H、N、T、C、K、J，故可假设密文字符X对应的明文字符为E，密文字符H对应的明文字符为T。

步骤2：单击“Simple Analysis”工具条中的“Affine”按钮，输入上述字母对，如图3-26所示。

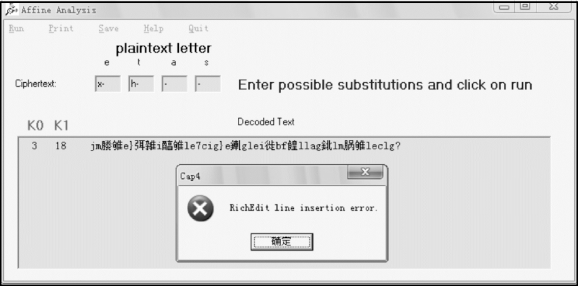
图3-26　验证猜测（1）

注意：设仿射函数为y＝k1x＋k0 mod 26，所以k1的取值只能属于下列整数集合{1，3，5，7，9，11，15，17，19，21，23，25}。很明显，以上猜测有误，故可以进一步假设密文字母X对应的明文字符为E，密文字符N对应的明文字符为T，经测试可知，该猜测也不成立。接着测试可以发现密文字符X对应明文字符E，密文字符T对应明文字符T的假设也不成立。试假设密文字符C对应明文字符T。

步骤3：进一步验证上述猜测，其结果如图3-27所示。

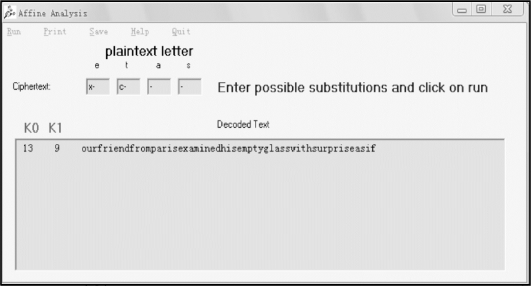
图3-27　验证猜测（2）

通过测试发现，此次假设成立，即该段密文采用的仿射变换函数可能为y＝9x＋13 mod 26。

步骤4：采用上述假设结果，选择“Cipher”→“Affine”选项，破解密文，如图3-28所示。

采用以上猜测结果破解密文所获取的明文具有意义，所以可以认定该次加密操作采用的加密变换函数为y＝9x＋13 mod 26。

图3-28　破解密文