分情境参数估计优化方案

为验证不同好评率下的购买意愿影响机理的差异，本研究以基准评论页面的好评率（即rate=60%）为分界线，将实验数据分成两个情境：低好评率情景和高好评率情景。

1.描述性统计分析

1）低好评率情景

此情景下样本数据的好评率均小于60%，即rate＜60%，共有样本51个。低好评率情境下样本的统计描述如表4-4所示。

表4-4　低好评率样本的统计描述

2）高好评率情境

此情景下样本数据的好评率均大于等于60%，即rate≥60%，共有样本55个。高好评率情境下样本的统计描述如表4-5所示。

表4-5　高好评率样本的统计描述

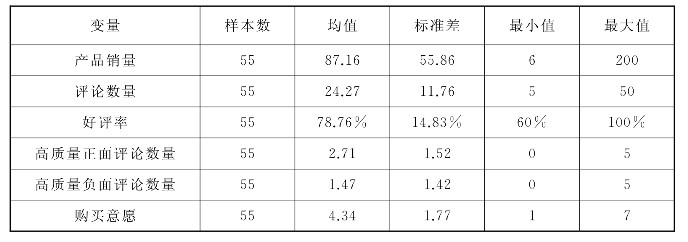
对表4-4和表4-5进行比较，可以发现在高好评率情境下，购买意愿的均值为4.34，显著大于低好评率情境下的2.20。同时高好评率情境下，购买意愿的标准差为1.77，大于低好评率情境下的1.51，说明在高好评率情境下，购买意愿的变化幅度更大。

2.回归分析

从统计描述中我们只能得到粗略的表明现象，更为深入的结论，还需要通过多元回归分析获得。为此本书以回归方程式（4-2）为原始模型，分别对两个情境进行回归分析，回归结果如下：(www.xing528.com)

1）低好评率情景

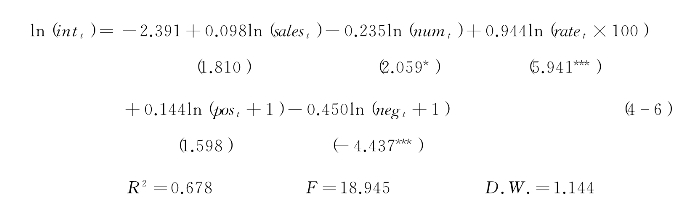
回归方程式（4-6）为低好评率情境下的原始模型回归结果，对回归结果进行各项统计检验，发现变量ln（salet）和ln（post+1）都对ln（intt）的影响不显著，在排除了模型存在多重共线性、自相关性以及异方差性后，对模型中不显著参数进行逐步删减，发现当删除ln（post+1）后，模型回归结果如方程（4-7）所示。

此时模型可决系数R2为0.657，相比于回归方程式（4-6）模型拟合稍有下降。但回归方程式的显著性和解释变量的显著性检验都得到了明显改善，故认为此模型为低好评率情境下的最终模型。

2）高好评率情境

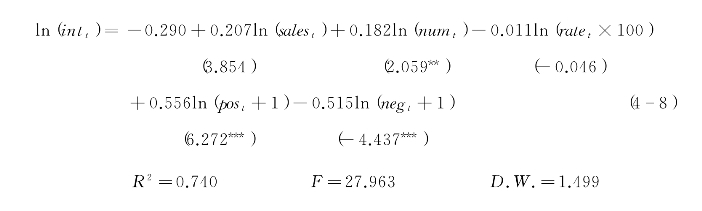
回归方程式（4-8）为高好评率情境下的原始模型回归结果，对回归结果进行各项统计检验，发现只有ln（ratet×100）对ln（intt）的影响不显著。对模型进行多重共线性、自相关性以及异方差性检验后，发现模型存在异方差性，于是对模型采用加权最小二乘法进行回归，回归结果显示，在消除了异方差性的情况下，ln（ratet×100）对ln（intt）的影响仍然不显著。因此在原始模型中删除ln（ratet×100），并采用最小二乘法对其进行回归，回归结果如方程式（4-9）所示，同时方程式（4-9）回归结果的可决系数R2仍为0.740，相比于原模型拟合度没有改变，但回归方程式的显著性和解释变量的显著性检验都得到了明显改善。

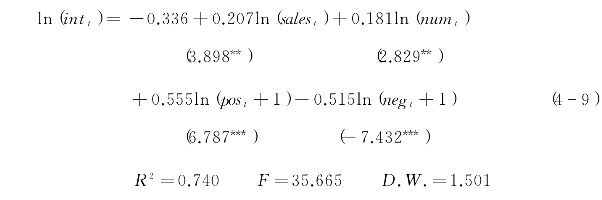
最后对所估计的模型再进行怀特检验，其结果如图4-8所示，可发现nR2对应值的伴随概率值较大，所以接受不存在异方差的原假设，即认为已经消除了模型的异方差性，说明模型的异方差性主要是由ln（ratet×100）造成的，某种程度上证明了我们之前的推理，即好评率较高时，消费者的购买意愿既可能较高也可能较低，整体的变化幅度很大。综合以上因素，故认为方程式（4-9）为高好评率情境下的最终模型。

图4-8　回归方程式（4-9）怀特检验的输出结果

Heteroskedasticity　Test：White