如何进行异方差检验和修正

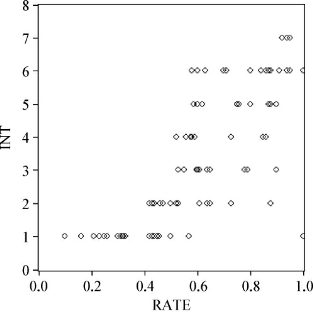
图4-4　好评率和购买意愿的散点图

异方差是指模型违反了经典假设中的同方差性，即对于不同的样本点，随机干扰项的方差不再是常数，而是互不相同。在存在异方差的情况下，如果仍然采用普通最小二乘估计模型参数，会导致参数估计值的非有效性和限制性检验无意义。

1.异方差检验

首先，用图示法检验。图4-4为好评率和购买意愿的散点图，从该图可发现，当好评率较低时，消费者的购买意愿也很低，很少出现高购买意愿的情况。但好评率较高时，消费者的购买意愿并不一定就很高，也可能很低，整体的变化幅度很大，即购买意愿的方差可能会随着好评率的上升而增大。

图4-5为ln（int）和残差平方散点图，可以看出残差平方项E2对解释变量ln（int）的散点图主要分布于图形中的下三角部分，大致看出残差平方项E2随ln（int）的变动呈减小的趋势，因此模型很可能存在异方差。

通过图示法，我们只能判断模型可能存在异方差，但是否确实存在异方差还应通过更进一步的检验。为此本研究采用怀特检验（White检验）来对方程式（4-4）的回归结果进行更进一步的异方差检验。Eviews软件可为回归方程直接输出怀特检验结果，如图4-6所示。

图4-5　ln（int）和残差平方散点图

图4-6　Eviews中怀特检验的输出结果(www.xing528.com)

Heteroskedasticity Test：White

由图4-6中的结果得到怀特统计量nR2=24.74，查χ2分布表得到在5%的显著性水平下，自由度为14的χ2分布的临界值为23.7。因为nR2=24.74＞23.7，所以拒绝同方差的原假设，模型存在异方差。

2.异方差修正

为了消除或减弱异方差性对模型的影响，提高估计参数的精度，运用加权最小二乘法的方法来对模型进一步优化。通过测试发现，将残差平方的倒数（即1/E2）作为加权最小二乘法的权变数量，效果最好。结果如下：

对所估计的模型再进行怀特检验，其结果如图4-7所示，可发现nR2对应值的伴随概率值较大，所以接受不存在异方差的原假设，即认为已经消除了模型的异方差性。

图4-7　回归方程式（4-5）怀特检验的输出结果

Heteroskedasticity Test：White

最后，将回归方程式（4-5）和式（4-3）、式（4-4）进行比较发现，模型经过异方差修正后，模型可决系数、回归方程的显著性以及解释变量的显著性检验都得到了显著提高，达到了极佳水平，因此可认为回归方程式（4-5）为最终模型。