【摘要】:如果违背这一假定,即线性回归模型中存在多重共线性。多重共线性会给普通最小二乘法带来参数估计量不存在、参数估计量经济含义不合理、变量的显著性检验失去意义等严重后果。本章的数据全部来自实验,所有解释变量的数据都是随机产生的,因此很好地避免了多重共线性。并通过观察变量间的相关系数,来进一步排除多重共线性的存在。
在多元线性回归模型经典假设中,其重要假定之一是回归模型的解释变量之间不存在线性关系,也就是说,任何一个解释变量都不能是其他解释变量的线性组合。如果违背这一假定,即线性回归模型中存在多重共线性。多重共线性会给普通最小二乘法带来参数估计量不存在、参数估计量经济含义不合理、变量的显著性检验失去意义等严重后果。
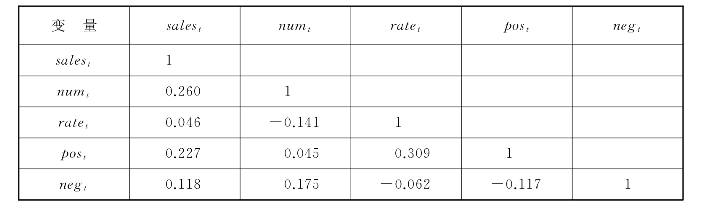
由于方程式(4-3)的回归结果显示评论数量对购买意愿的影响不显著,为此我们首先要考虑评论数量和其他解释变量是否存在多重共线性。本章的数据全部来自实验,所有解释变量的数据都是随机产生的,因此很好地避免了多重共线性。并通过观察变量间的相关系数,来进一步排除多重共线性的存在。表4-3为相关系数矩阵,从该表中可知,本研究中所有变量两两之间相关系数均在0.4以下,而一般情况下大于0.8才被认为线性相关,因此不存在多重共线性,从而说明评论数量对购买意愿在理论上可能就没有影响。为此,本章把变量ln(numt)从模型中剔除,得到回归方程式(4-4)。
表4-3 相关系数矩阵(https://www.xing528.com)
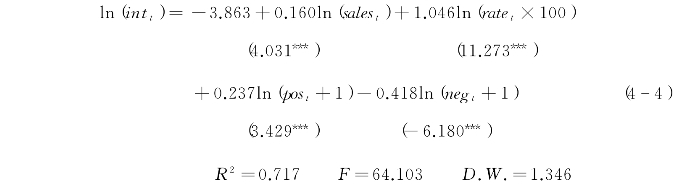
从回归方程式(4-4)估计的结果可以看出,模型可决系数R2为0.717。相比回归方程式(4-3),模型拟合没有改进,但回归方程的显著性和解释变量的显著性检验都得到了明显改善。为了提高可决系数,使拟合优度更好,回归方程式(4-4)还需要更进一步检验和修正。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




