假设检验结果表明产品卷入度存在显著差异

1.模型修正与探索

运用AMOS　18.0软件，采用极大似然估计法对结构方程模型进行估计，其中外生变量之间的相关性设为自由相关，图3-5为原始模型的路径系数，表3-10为模型的拟合输出结果。

图3-5　在线评论采纳原始模型的路径系数

表3-10　在线评论采纳原始模型拟合指数

如表3-10所示，原始模型中，除χ2/df、CFI的拟合效果较好，其他指数均没有达到评价标准，说明整体的拟合效果不太好。

为此，首先根据AMOS　18.0软件的输出报告增加残差间相关关系来对初始模型进行微调；其次删除不显著的路径，一次修改一条路径，将不显著的路径关系一一删除，并仔细观察相关指数的变化，避免同时操作多条路径可能造成的误差，最后得到修正模型的路径系数和拟合指数。由图3-5可以看出，在模型的9条待检验关系中，只有2条没有通过检验，分别为：相关性→评论有用性（β=-0.016，p＜0.05），及时性→评论有用性（β=0.020，p＜0.05）。因此我们逐步删除这2条路径。

最终得到修正模型的路径系数，如图3-6所示。

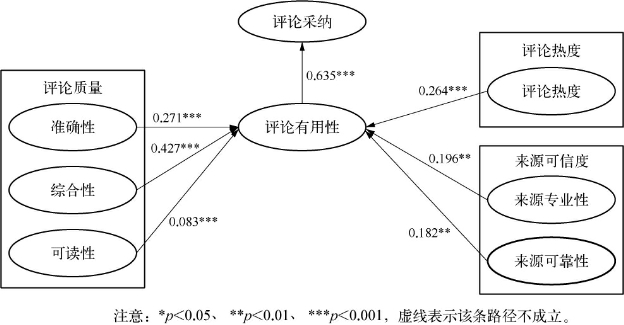
图3-6　在线评论采纳修正模型的路径系数

修正模型的拟合指数，如表3-11所示。参照模型拟合的标准，各项拟合指数都达到标准，可以认为模型拟合结果较好。

表3-11　在线评论采纳修正模型拟合指数

2.产品卷入度的调节作用

结构方程模型是分析潜变量调节效应的一种有效工具，而调节效应可以理解为：根据调节变量分类的不同样本群组，在进行模型检验时，模型的路径系数不同。因此本书拟采用结构方程的多群组分析来检验产品卷入度的调节作用。多群组分析是一种结构方程的架构，其功能在于检验相似模型在不同群组受试间的差异。借鉴吴明隆（2013）关于在AMOS中进行多群组比较的策略［98］，本书采用如下做法：

第一步：将所有样本按照调节变量分成两组。

本书用K-Means方法进行聚类分析，将样本按产品卷入度的高低将产品分成两类，结果如表3-12所示。

表3-12　K-Means聚类分析结果

(www.xing528.com)

随后对分组后的样本进行独立样本T检验。T检验结果显示产品卷入度差异显著，说明两类样本的产品卷入度存在显著不同。

第二步：分类建立初始模型。分别对两类样本数据进行结构方程模型分析。

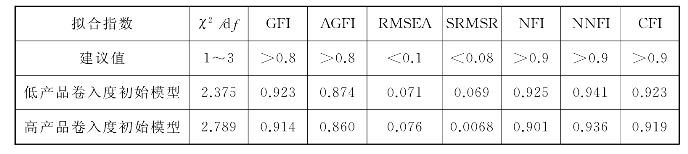
此步骤中，由于评论的相关性、及时性与评论有用性的关系在上文中未得到证实，因此我们只需验证评论质量中准确性、综合性和可读性在两组样本下对评论有用性影响的差异。图3-7和图3-8分别为低产品卷入度和高产品卷入度情景下的初始模型路径系数。两初始模型中均未出现大于1的标准化路径系数，表示模型的估计参数均为适当的解。表3-13为两个模型的拟合指数。参照模型拟合的标准，整体而言，各项拟合指数都达到标准，可以认为模型拟合结果较好。

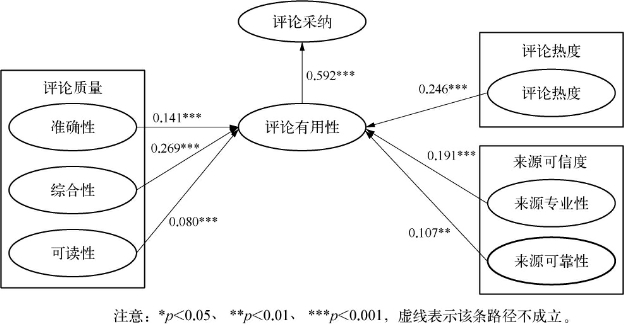
图3-7　低产品卷入度初始模型的路径系数

图3-8　高产品卷入度初始模型的路径系数

表3-13　基线模型拟合指数

第三步：建立多群组分析模型图与模型估计。甄别单个群组模型图的标准化路径系数是否出现不合理参数，检验卡方自由度比值、GFI、AGFI、RMSEA、SRMSR、NFI、NNFI、CFI等模型拟合指数，来判断假设模型在两个不同群组间是否具有结构不变性。

本书利用AMOS　18.0进行多群组模型分析。低产品卷入度、高产品卷入度的单群组分析与多群组分析的主要拟合指数如表3-14所示。

表3-14　多群组分析的拟合指数

如表3-14所示，多群组假设模型的拟合指数达到模型拟合标准，表示假设模型具有群组等同性，此因果模型的假设模型在不同产品卷入度群组中有结构不变性。

第四步：多群组分析的竞争模型。多群组分析中若未受限制模型（即本书的多群组初始模型）可以被接受，则将两组的结构方程回归系数限制为相等（简称受限制模型），将其与未受限制模型进行差异检验，若两个模型卡方值的差异量达到显著，则认为受限制模型不为真，即认为两个群组的结构方程模型有不同的路径系数。

当样本数量较大时，卡方值的差异量也会较大，很容易达到显著水平（显著值p＜0.05），因而还需要参考4个较不受模型复杂度影响的适配度统计量，这4个统计量分别为NFI、IFI、RFI、NNFI（TLI）。如果上述4个统计量的差异的绝对值大于0.05，表示两个群组的结构方程模型有不同的路径系数。表3-15呈现了多群组初始模型和受限制模型的拟合指数。

表3-15　未受限制模型和受限制模型的拟合指数比较

从表3-15可知，受限制模型增值拟合指数均大于0.90，并且未受限制模型（多群组初级模型）与受限制模型NFI、RFI、IFI、NNFI的差异分别为0.004、-0.002、-0.003、-0.001，绝对值均小于0.05，表示未受限制模型（多群组初始模型）为正确模型时，受限制模型也为正确。即说明产品卷入度的调节效应不显著，从而拒绝假设H10c、H11c、H12c、H13c和H14c。