历史成本分析法的应用和技巧

历史成本法是根据企业以往若干时期的成本与业务量的相关历史资料，运用数学方法进行数据处理，以完成成本性态分析任务的一种定量分析的方法。这类方法是混合成本分解最常用的方法之一。该方法要求企业的历史资料比较齐全，成本数据和业务量资料要同期配套，有相关性。

常用的历史成本分析法有高低点法、散布图法、回归分析法3种，如图2.15所示。

图2.15　常用的历史成本分析

1）高低点法

高低点法又称两点法，是指通过观察一定相关范围内的各期业务量与相关成本构成的所有坐标点，从中选出高低两点坐标，并据此来推断固定成本a和变动成本b的一种成本性态分析方法。注意：高点和低点指的是业务量的高低。

（1）高低点法步骤

①收集历史数据，找到特定时期对应的最高业务量水平和最低业务量水平及其分别对应的成本。

②计算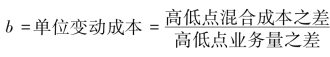差。

③将b代入高点或者低点方程求出a。

④将a和b代入y=a+bx，得出成本分解模型。

（2）高低点法举例

【例2.2】　客满意公司1—5月产量和每月维修费之间的关系见表2.4。

要求：用高低点法对其成本每月维修费进行成本性态分析。

表2.4　产量与维修费用表

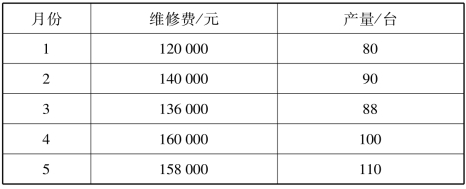
解：由表2.4可知，产量最高点110台（5月）和最低点80台（1月）相应的维修成本为158 000元和120 000元。根据这两组数据，计算单位变动成本为

每月固定成本a=158 000元﹣1 267元/台×110台=18 630元则维修费成本模型为

y=18 630+1 267 x

技能训练1

继［例2.2］，假设3月维修费为180 000元，对应产量为120台，其他条件不变，要求用高低点法对维修费进行成本性态分析。

2）散布图法

散布图法是将一定时期的混合成本历史数据，逐一在坐标图上标明以形成散布图，然后通过目测，在各个成本点之间做出一条反映成本变动平均趋势的直线，借以确定混合成本中变动成本和固定成本的方法，最终得到成本模型。

（1）散布图法的具体步骤

①标出散布点。将各期业务量和相应成本的历史资料作为点的坐标标注在坐标图上。

②画线。通过目测画一条直线，使其尽可能通过或接近所有坐标点。

③在纵坐标上读出该直线的截距值，即固定成本a。

④在该直线上任取一点p，假设其坐标值为（x，y），将其代入下式计算单位变动成本。

⑤。

⑥将a值和b值代入下式，建立成本性态模型y=a+bx。

（2）散布图法举例

【例2.3】　客满意公司2017年1—12月维修成本的历史数据见表2.5，要求用散布图法确定其维修成本进行分解并建立成本性态模型。

表2.5　维修成本数据表

解：首先以机器工作小时数为x与维修成本y在坐标轴描点。

然后以描出来点化一条成本趋势直线，画出该成本趋势直线与y轴的交点为500，则表示该成本函数的固定成本a=500元。

最后在直线上任取一点，如x=1 300，此时y=910，则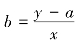代入后可得

据此可维修成本性态模型为：y=500+0.32x，如图2.16所示。

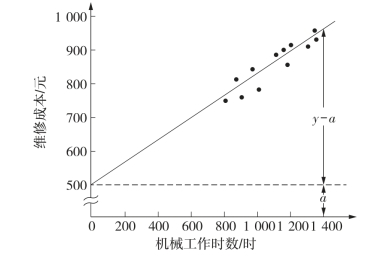
图2.16　维修成本性态模型散布图

技能训练2(www.xing528.com)

继［例2.3］，假设1月机器工作数为1 000小时，对应的维修成本为850元，12月机器工作数为1 500小时，对应的维修成本为960元。

要求：用散布图法对维修成本进行成本性态分析。

3）回归分析法

上述散布图法是通过目测的方法来勾画混合成本的性态的。不同的人会勾画出不同的直线，而且很难判断出哪条直线更为准确。回归分析法则是运用数理统计中常用的最小平方法的原理，对所观察到的全部数据加以计算，从而画出最能代表平均水平的直线。

这条通过回归分析而得到的直线则称回归直线。它的截距就是固定成本，斜率就是单位变动成本。因为回归分析法可以使各观察到的数据与直线相应各点的误差的平方和实现最小化，也称最小二乘法。因此，回归分析法又称最小平方法。

（1）回归分析法公式

根据过去一定时期的业务量和成本资料，建立反映成本和业务量之间关系的回归直线方程，并据此确定成本中的固定成本和变动成本的一种成本性态分析方法。

设共有n期业务量x和成本y的资料，每期资料的x，y之间的关系可用直线方程y=a+bx表示。根据资料求得a，b的值。其计算公式如下：

回归分析法中a，b值的计算公式

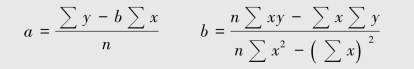
值得注意的是：只有x，y呈现显著相关时（即x，y之间有很强的相关性）如身高和体重两个变量。一般来说，身高越高的人体重越重，即代表两者相关，这种回归分析才有意义。

（2）回归分析法的步骤

①根据历史资料列表求出n，∑x，∑y，∑xy，∑x2，∑y2的值。

②计算相关系数r，并据此判断x与y的相关性。其计算公式如下：

回归分析法中相关系数r的计算公式

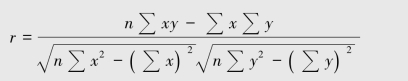
③如果r=1或者r→1，则说明x与y正相关或基本正相关，存在线性关系，则根据公式可算出固定成本a及单位变动成本b。

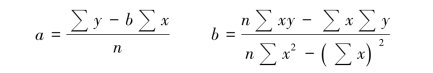
④代入a，b建立成本性态模型为y=a+bx。

（3）回归分析法举例

【例2.4】　客满意公司销售量和销售成本资料见表2.6，要求用回归分析法对销售成本进行成本性态分析并建立成本模型。

表2.6　销售量（万台）与销售成本（万元）表

解：首先计算相关系数r，判断销售量与销售成本间是否具有相关性。

代入相关系数公式

可算出相关系数r=0.94。

可见销售量与销售成本间有很强的线性相关关系，则可以用回归分析法来分解混合销售成本。

再计算单位变动成本b，固定成本a，再代入成本回归方程：

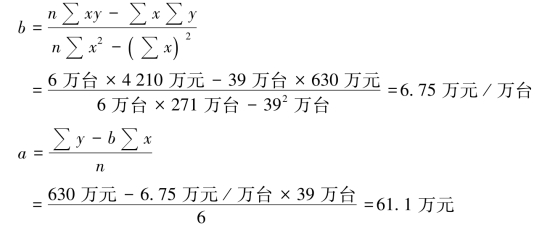
回归分析法的原理

则建立成本模型为

y=61.1+6.75 x

技能训练3

继［例2.4］，假设2月销售量为9万台，销售成本为112万元，6月销售量为10万台，销售成本为130万元，其他条件不变，要求用回归分析法对销售成本进行成本性态分析并建立成本模型。

4）3种历史成本法比较

3种历史成本法都是运用历史成本数据，经过适当数学方法对其进行处理，从而分解出固定成本和单位变动成本的定量分析方法，通过上述的讲解可以看出它们各自有不同的优缺点，见表2.7。

表2.7　3种历史成本法比较

想一想：

历史成本分析法有哪几种常用的方法？它们的适用范围是什么？