风险调整贴现率法：解决投资风险和净现金流问题的决策方法

在不考虑通货膨胀的情况下，风险调整贴现率法是将无风险报酬率调整为考虑风险的投资报酬率（即风险调整贴现率），然后根据风险调整率贴现率来计算净现值并据此选择投资方案的决策方法。这种方法的基本思路就是，对于高风险的项目必须要有高的贴现率，对于低风险的项目必须采用低的贴现率。所以风险调整贴现率法主要解决两个问题：一是投资项目风险程度大小如何确定；二是风险报酬斜率如何确定。解决了这两个问题后，风险报酬的贴现率就能计算出来。

根据第二章第二节讨论的内容已知：

假如用K表示风险调整贴现率，i表示无风险报酬率，b表示风险报酬斜率，Q表示风险程度，则上式可以表示为：

下面我们通过一个例子来说明怎样计算风险程度、风险报酬斜率，以及根据风险调整贴现率法来选择最佳方案。

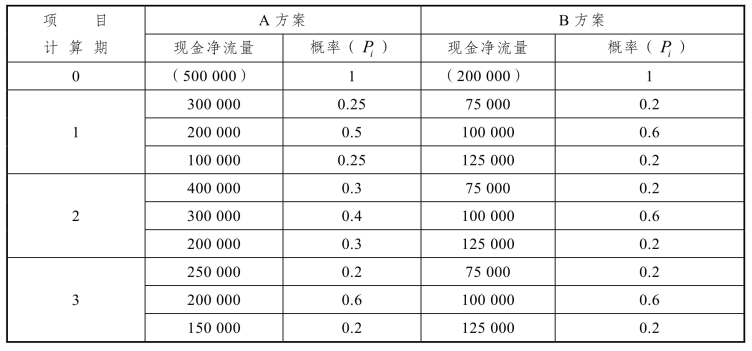
【例4-24】某企业的无风险报酬率为5%，现有两个投资方案，有关资料如表4-7所示。

要求：采用风险调整贴现率法来选择哪一方案。

表4-7　投资方案的相关资料　单位：元

解：具体计算步骤如下：

（1）确定风险程度Q。

① 计算投资方案各年现金净流量的期望值tE。

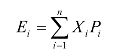
本例的风险因素全部在经营期的NCF之中，有三种可能，并且已知了概率，但并不意味着建设期的NCF没有风险，而只是为了简化。

A方案：

B方案：

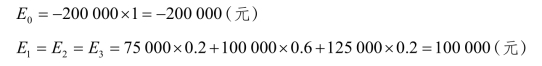
② 计算反映各年现金净流量离散程度的标准差td。

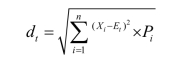
A方案：

B方案：

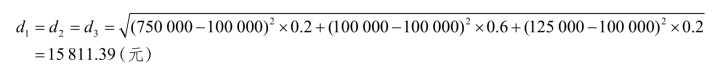
标准差越大，说明现金净流量分布的离散程度越大，风险就越大；反之，风险越小。用标准差反映现金净流量的不确定性即风险的大小是很重要的，但也存在一定的局限性。因为标准差是一个绝对值，不便于比较期望值不同的决策方案风险的大小。因此，还需计算标准差系数，即标准离差率。

③ 计算标准差系数tq。(www.xing528.com)

上述计算只反映了某一年的风险大小，为了综合各年的风险，还需计算综合的标准差系数。

④ 计算综合标准差系数Q。

式中，D为综合标准差，其计算公式为：

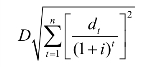
EPV为各年期望值的现值之和，其计算公式为：

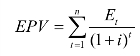
A方案：

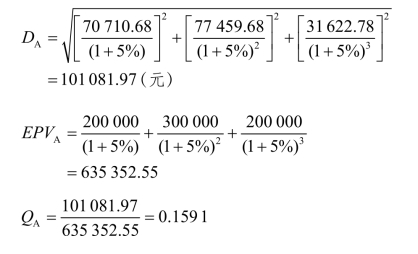
B方案：

（2）确定风险报酬斜率b。

风险报酬斜率b的高低反映了风险程度变化对风险调整贴现率影响的大小，其数值的大小可以根据历史资料用高低点法或直线回归法求出，也可以由企业领导或有关专家根据经验数据确定。

假定该企业过去五项投资的投资报酬率和标准差系数之间的关系如表4-8所示。

表4-8　投资报酬率和标准差系数的关系

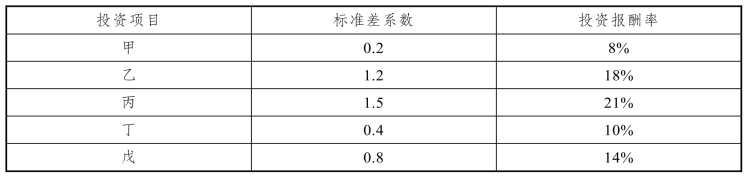
根据直线方程K=i+b×Q ，采用高低点法来确定b。

（3）计算风险调整贴现率K。

根据K=i+b×Q ，得出：

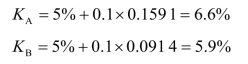
（4）根据风险调整贴现率计算投资方案的净现值，其计算公式为：

考虑了风险价值后，A方案的净现值116 723.51元大于B方案的净现值67 796.51元，但是，A、B方案的投资额不相等，用净现值指标进行方案之间的选择不妥，所以应用净现值率这一相对数指标进行决策，A方案的净现值率0.233 4小于B方案的净现值率0.339 0，因此，应选择B方案进行投资。

风险调整贴现率法对风险大的项目采用较高的贴现率，对风险小的项目采用比较低的贴现率，理论比较完善，便于理解，使用广泛。但是这种方法把时间价值和风险价值混淆在一起，对每年的现金流量进行贴现，意味着风险随着时间的推移而加大。这种假设有时与实际情况不符，也是风险调整贴现率法的局限性。