如何正确衡量风险：标准差系数的应用

由于风险具有普遍性和广泛性，那么正确地衡量风险就十分必要。既然风险是可能值对期望值的偏离，因此利用概率分布、期望值和标准差来计算与衡量风险的大小，是一种最常用的方法。

（一）概率

在完全相同的条件下，某一事件可能发生也可能不发生，可能出现这种结果也可能出现另外一种结果，这类事件称为随机事件。概率就是用来反映随机事件发生的可能性大小的数值，一般用X表示随机事件，Xi表示随机事件的第i种结果，Pi表示第i种结果出现的概率。一般随机事件的概率在0与1之间，即0≤Pi≤1，Pi越大，表示该事件发生的可能性越大；反之，Pi越小，表示该事件发生的可能性越小。所有可能的结果出现的概率之和一定为1，即ΣPi=1。肯定发生的事件的概率为1，肯定不发生的事件的概率为0。

【例2-17】某企业投资生产了一种新产品，在不同市场情况下，各种可能收益及概率如表2-1所示。

表2-1　新产品的年收益及概率

从表2-1中可见，所有的Pi均在0和1之间，且P1+P2+P3=0.3+0.5+0.2=1。

如果我们将该企业年收益的各种可能结果及相应的各种结果出现的概率按一定规则排列出来，构成分布图，则称为概率分布。概率分布一般用坐标图来反映，横坐标表示某一事件的结果，纵坐标表示每一结果相应的概率。概率分布有两种类型：一是离散型概率分布，其特点是各种可能结果只有有限个值，概率分布在各个特定点上，是不连续图像（见图2-6）；二是连续型概率分布，其特点是各种可能结果有无数个值，概率分布在连续图像上的两点之间的区间上（见图2-7）。

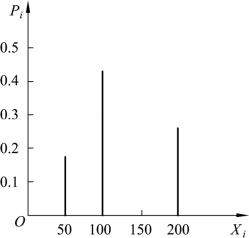
图2-6　离散型概率分布　

图2-7　连续型概率分布

（二）期望值

期望值是指可能发生的结果与各自概率之积的加权平均值，反映投资者的合理预期，用E表示。根据概率统计知识，一个随机变量的期望值为：

【例2-18】利用例2-17中的资料。

要求：计算预期年收益的期望值。(www.xing528.com)

解：E=200×0.3+100×0.5+50×0.2=120（万元）

（三）标准差

标准差是用来衡量概率分布中各种可能值对期望值的偏离程度，反映风险的大小，用σ表示。

标准差的计算公式为：

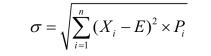
标准差用来反映决策方案的风险，是一个绝对数。在n种方案的情况下，若期望值相同，则标准差越大，表明各种可能值偏离期望值的幅度越大，结果的不确定性越大，风险也越大；反之，标准差越小，表明各种可能值偏离期望值的幅度越小，结果的不确定越小，则风险也越小。

【例2-19】利用例2-17的数据，计算标准差。

新产品的年收益与期望收益的标准差为55.68。

（四）标准差系数

标准差作为反映可能值与期望值偏离程度的一个指标，可用来衡量风险，但它只适用于在期望值相同条件下风险程度的比较，对于期望值不同的决策方案，则不适用。于是，我们引入标准差系数这个概念。

标准差系数是指标准差与期望值的比值，也称离散系数，用q表示。其计算公式如下：

标准差系数是一个相对数，在期望值不同时，标准差系数越大，表明可能值与期望值偏离程度越大，结果的不确定性越大，风险也越大；反之，标准差系数越小，表明可能值与期望值偏离程度越小，结果的不确定性越小，风险也越小。

【例2-20】利用例2-17的数据，计算标准差系数。

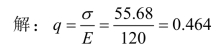
有了期望值和标准差系数，我们可利用这两个指标来确定方案风险的大小，选择决策方案。对于单个方案，可将标准差（系数）与设定的可接受的此项指标最高限值进行比较；对于多个方案，选择标准差低、期望值高的方案，具体情况还要具体分析。