按照经济学理论,生产厂家在进行生产时所投入的生产要素可以分为固定投入和可变投入。固定投入如机器、厂房等;可变投入如原料、劳动等。在分析生产要素和产量的关系时,我们先从最简单的一种生产要素的投入开始,即在其他生产要素投入不变的情况下,只有一种生产要素的投入量是可以变化的,这种可变的生产要素的不同投入水平会有不同的产量水平。那么这种可变要素的最佳合理投入水平应该如何确定?
一、总产量、平均产量和边际产量
总产量(TP)是指与投入一定量的可变生产要素相对应的最大产量。如在一块麦田中雇佣2个农民,生产出400公斤小麦,则400公斤小麦就是雇佣2个农民的总产量。用公式表示为:
TP=f(L)
平均产量(AP)是指每单位生产要素的平均产出量。如上例中,每个农民的平均产量就是200公斤。如果用L表示生产要素的投入量,那么平均产量可用公式表示为:
![]()
边际产量(MP)是指每增加一单位生产要素投入量所带来的总产量的增加量。如上例中,如果小麦田里再增加1个农民,小麦产量便又增加了20公斤,则20公斤小麦是第3个农民的边际产量。如果用ΔTP表示总产量的变化量,ΔL表示生产要素的变化量,那么边际产量可用公式表示为:
![]()
二、总产量、平均产量和边际产量的相互关系
假定在某产品生产过程中所使用的生产要素是资本和劳动,其中资本的投入量是固定不变的,劳动的投入量是可变的。根据上述关系作表6-1。
表6-1 劳动投入与总产量、平均产量以及边际产量之间的关系
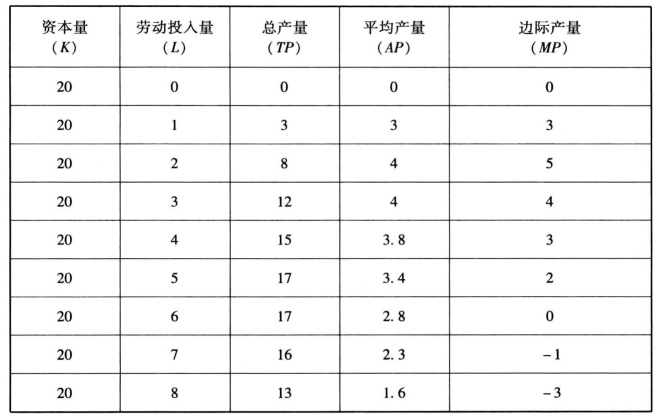
根据表6-1,可以作出图6-1。
在图6-1中,横轴代表劳动投入量,纵轴代表产量。TP为总产量曲线,AP为平均产量曲线,MP为边际产量曲线。三条产量曲线分别表示随着劳动投入量的不断增加,各种产量的变动趋势。N为总产量曲线的拐点,对应于边际产量递增与递减的转折点。S为总产量曲线的切点,对应于边际产量与平均产量相交的点。R为总产量曲线的最大点,对应于边际产量为零的点。
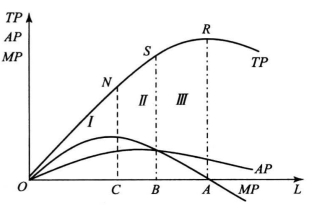
图6-1 总产量、平均产量和边际产量之间的关系
根据图6-1,可以看出总产量、平均产量和边际产量之间的关系有如下特点:
(1)总产量与平均产量的关系。从图6-1可以看出,总产量曲线先以递增的速度增加,到拐点N以后,以递减的速度增加,过最大点R后变为递减。在O到B之间,随着劳动投入的增加,总产量随之不断增加,与之相适应的平均产量也不断增大,在B点,平均产量达到极大值,在B点以后,随着劳动投入的继续增加,总产量先以递减速度增加而后减少,与之相适应的平均产量则减少。
(2)总产量与边际产量的关系。从图6-1可以看到,总产量与边际产量之间有对应关系。在O到C之间,随着劳动投入的增加,总产量以递增速度增加,与之相适应的边际产量也不断增大,到了C对应点,边际产量最大。在C到A之间,随着劳动投入的继续增加,总产量以递减速度增加,与之相适应的边际产量减少,到了A对应点,总产量最大。过了A对应点以后,随着劳动投入的继续增加,总产量递减,与之相适应的边际产量负值。
(3)平均产量与边际产量的关系。从图6-1可以看出,边际产量曲线通过平均产量曲线的最高点。在B点左边,边际产量大于平均产量,平均产量递增。在B点右边,边际产量小于平均产量,平均产量递减。在B点,边际产量等于平均产量,平均产量最大。
【知识链接】
经济学十大原理之——理性人考虑边际量
生活中的许多决策涉及对现有行动计划进行微小的增量调整,经济学家把这些调整称为边际变动。在许多情况下,人们可通过考虑边际量来作出最优决策。
例如,假设一位朋友请教你,他应该在学校上多少年学。如果你给他用一个拥有博士学位的人的生活方式与一个没有上完小学的人进行比较,他会抱怨这种比较无助于他的决策。你的朋友很可能已经受过某种程度的教育,并要决定是否再多上一两年学,为了作出这种决策,他需要知道,多上一年学所带来的额外收益和所花费的额外成本。通过比较这种边际收益与边际成本,他就可以评价多上一年学是否值得。
再举一个考虑边际量如何有助于作出决策的例子,考虑一个航空公司决定对退票的乘客收取多高的价格。假设一架200个座位的飞机横越国内飞行一次,航空公司的成本是10万美元。在这种情况下,每个座位的平均成本是500美元,有人会得出结论:航空公司的票价决不应该低于500美元。
但航空公司可以通过考虑边际量而增加利润。假设一架飞机即将起飞时仍有10个空位。在登机口等退票的乘客愿意支付300美元买一张票。航空公司应该卖给他票吗?当然应该。如果飞机有空位,多增加一位乘客的成本是微乎其微的。虽然一位乘客飞行的平均成本是500美元,但边际成本仅仅是这位额外的乘客将消费的一包花生米和一罐汽水的成本而已。只要等退票的乘客所支付的钱大于边际成本,卖给他机票就是有利可图的。(https://www.xing528.com)
正如这些例子说明的,个人和企业通过考虑边际量将会作出更好的决策。只有一种行动的边际收益大于边际成本,一个理性决策者才会采取这项行动。
三、生产三阶段与一种可变生产要素的合理投入
根据总产量、平均产量和边际产量的关系,我们可以把图6-1划分成三个区域,表示可变生产要素的三个投入阶段。
第一个阶段(Ⅰ)是劳动投入量从零增加到B点的阶段。在这一阶段,随着劳动投入的不断增加,总产量在不断增加,平均产量也在不断增加。说明在这一阶段,相对于不变的资本量而言劳动投入量不足,所以劳动投入量的增加可以使资本利用效率越来越高,不但总产量可以增加,而且劳动生产率,也就是劳动的平均产量也是递增的。由此看来,劳动投入量不应该停止在第一个阶段,而至少要增加到B点为止。否则,资本的利用效率就不充分。
第二个阶段(Ⅱ)是劳动投入量从B点到A点的阶段。在这一阶段,随着劳动投入的不断增加,不变的资本越来越接近被充分利用。然而,由于劳动生产率在这一阶段开始下降,平均产量则开始递减。在这一阶段,虽然边际产量继续下降,但还是正值,因而总产量还是在不断增加,只是增加的幅度越来越小。在劳动量增加到A点时,总产量可以达到最高。
第三个阶段(Ⅲ)是劳动投入量超过A点以后的阶段。在这一阶段,随着劳动投入的继续增加,不变的资本已经被完全充分利用,已经不再有增加产量的潜力。在这一阶段,不但平均产量在继续下降,而且边际产量已成为负值,也就是总产量开始绝对减少。很显然,劳动投入量超过A点之后是不利的。
综合上述分析,合理的劳动投入水平既不应该在生产的第一阶段,也不应该在生产的第三阶段,而只应该在生产的第二阶段,即在B点和A点之间。但劳动投入量应该在第二阶段的哪一点上,则要结合厂商的生产目标来具体分析。
例如,如果企业将生产目标定为平均产量最大,这时应将可变的生产要素投入量增加到B点;如果企业将生产目标定为总产量最大,这时应将可变的生产要素量增加到A点。一般而言,在市场经济条件下,厂商生产的目标既不是平均产量最大,也不是总产量最大,而是追求利润最大化。那么,在此情况下就要考虑成本、产品价格等因素。因为平均产量最大时,并不一定是利润最大;总产量最大时,利润也不一定最大。
四、边际产量递减规律
边际产量递减规律又称边际收益递减规律或者边际报酬递减规律。它的基本内容是:在技术水平和其他生产条件不变的前提下,当把一种可变的生产要素投入到一种或几种不变的生产要素中时,最初这种生产要素的增加会使产量增加,但当它的增加超过一定限度时,增加的产量将会递减,最终还会使产量绝对减少。例如,一个面包房有两个面包烤炉为其固定投入,当可变投入劳动从一个工人增加到两个时,面包烤炉得到充分利用,工人的边际产量递增,但如果工人的数量增加到3个、4个甚至更多时,几个工人共用一个面包烤炉,每个工人的边际产量自然会出现递减,甚至成为负数。
在理解边际产量递减规律时,要注意以下几点:
(1)这一规律发生作用的前提是技术水平不变。技术水平不变是指生产中所使用的技术没有发生重大变革。现在,技术进步的速度很快,但并不是每时每刻都有重大的技术突破,技术进步总是间歇式进行的,只有经过一定时期的准备之后才会有重大的突破。短期内无论是农业还是工业,一种技术水平一旦形成,总会有一个相对稳定的时期,这一时期就可以称为技术水平不变时期。
(2)这一规律所指的是生产中使用的生产要素分为可变的与不变的两类。边际产量递减规律研究的是把不断增加的一种可变生产要素,增加到其他不变的生产要素上时对产量所发生的影响。这种情况也是普遍存在的,例如,在农业中,当土地等生产要素不变时,增加施肥量;或者在工业中,当厂房、设备等生产要素不变时,增加劳动力都属于这种情况。
(3)在其他生产要素不变时,一种生产要素增加所引起的产量或收益的变动可以分为三个阶段:第一阶段表现为产量递增,即这种可变生产要素的增加使产量或收益增加。第二阶段表现为边际产量递减,即这种可变生产要素的增加仍可使总产量增加,但增加的比率,即增加的每一单位生产要素的边际产量是递减的。第三阶段表现为产量绝对减少,即这种可变生产要素的增加会使总产量减少。
边际产量递减规律是从科学实验和生产实践中得出来的,在农业中的作用最明显。早在1771年,英国农学家A·杨格就用在若干相同的地块上施以不同量肥料的实验,证明了肥料施用量与产量增加之间存在着这种边际产量递减的关系。以后,国内外学者又以大量事实证明了这一规律。这一规律同样存在于其他部门。工业部门中劳动力增加过多,会使生产率下降;行政部门中机构过多,人员过多也会降低行政办事效率,造成官僚主义。我国俗话所说的“一个和尚挑水吃,两个和尚抬水吃,三个和尚没水吃”,正是对边际产量递减规律的形象表述。
【经典案例】
三季稻不如两季稻
1958年“大跃进”是一个不讲理性的年代,时髦的口号是“人有多大胆,地有多高产”。于是一些地方把传统的两季稻改为三季稻,结果总产量反而减少了。从经济学的角度看,这是因为违背了一个最基本的经济规律:边际产量递减规律。
两季稻是农民长期生产经验的总结,它行之有效,说明在传统农业技术下,固定生产要素已经得到了充分利用。改为三季稻之后,土地过度利用引起肥力下降,设备、肥料、水利资源等由两次使用改为三次使用,每次使用的数量不足。这样,三季稻的总产量就低于两季稻了。
【延伸阅读】
马尔萨斯观察与边际产量递减规律
马尔萨斯极为关注农业边际产量递减规律的后果。根据他的分析,在土地供给数量和人口增加的条件下,每个额外生产者耕作的土地数量不断减少,他们所能提供的额外产出会下降;这样虽然食物总产出会不断增加,但是新增农民的边际产量会下降,因而社会范围内人均产量也会下降。在马尔萨斯看来,世界人口增加比例会大于食物供给增加比例。因此,除非能够说服人们少要孩子——马尔萨斯并不相信人口可以由此得到控制——否则饥荒将在所难免。
在马尔萨斯生活的时代,工业化进步尚未提供成熟的可以替代耕地的农业技术,能够大幅度提高单位耕地面积亩产,克服人多地少的经济内部农业和食物生产边际收益递减带来的困难。从实证分析角度看,马尔萨斯的理论建立在边际产量递减规律基础之上,对于观察工业化特定阶段的经济运行矛盾具有历史认识价值。换而言之,如果没有现代替代耕地的农业技术出现和推广,如果没有外部输入食物或向外部输出人口的可能性,英国和欧洲一些国家工业化确实会面临马尔萨斯陷阱所描述的困难。马尔萨斯观察暗含了农业技术不变与人均占有耕地面积下降这两点假设条件。如果实际历史和社会经济状况满足或接近这两个条件,马尔萨斯陷阱作为一个条件预测是有效的。例如,这一点对于认识中国经济史上某些现象具有分析意义。在我国几千年传统农业历史时期,农业技术不断改进,但没有突破性进步;在没有战乱和大范围饥荒的正常时期,人口长期增长率远远高于耕地面积增加速度。由于越来越多人口不得不在越来越小的人均耕地面积上劳作,劳动生产率和人均粮食产量难免下降。这一基本经济面的边际产量递减规律作用,加上其他一些因素(如制度因素导致的分配不平、外族入侵,等等)影响,可能是我国几千年传统农业社会周期振荡的重要原因。
然而,马尔萨斯结论作为一个无条件预言是错误的。近现代世界经济史告诉我们,过去200多年间,农业科学技术不断取得革命性突破,与马尔萨斯生活时代情况发生了根本性变化,与他的推托暗含的假设条件完全不同。化肥、机械、电力和其他能源、生物技术等现代技术和要素投入,极大地提高了农业劳动生产率,使农业和食品的增长率显著超过人口增长。从历史事实看,马尔萨斯理论是对边际收益规律的不适当运用。如果说马尔萨斯当年分析还有某种历史认识价值,那么形形色色的现代马尔萨斯预言则是完全错误的。
(资料来源:卢锋,《经济学原理》,北京大学出版社,2002年版,第79—80页。)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




