无差异曲线的含义及应用场景

无差异曲线是用来表示给消费者带来偏好相同的两种商品的所有数量组合的线。或者说，它是表示能够给消费者带来相同效用水平或满足程度的两种商品的所有组合的线。

假设某个消费者要面临着X、Y两种商品，这两种商品可以有A、B、C、D、E、F六种不同的消费组合，这六种组合都能给该消费者带来相同的效用，如表6－1所示。

表6－1　某消费者的效用无差异表

根据表6－1，可以绘制出图6－3。

在图6－3中，横轴代表商品X的数量，纵轴代表商品Y的数量，点A、B、C、D、E、F表示六种不同的商品组合，将各点连接起来的曲线I就是无差异曲线。无差异曲线上的任何一个点所表示的商品组合虽然都各不相同，但它们在消费者偏好既定的条件下给消费者所带来的效用，即满足程度都是相同的。

无差异曲线具有四个基本特征。

（1）在正常的消费阶段，无差异曲线是一条向右下方倾斜的曲线，其斜率为负值。这表明，在消费者消费两种商品的数量都达到饱和之前，也就是增加每一种商品的消费还都能给消费者带来正效用的条件下，消费者为了保证总效用不变，再增加一种商品的消费，就必须减少另一种商品的消费。

(www.xing528.com)

图6－3　无差异曲线

（2）同一平面上可以有无数条无差异曲线，如图6－4所示。我们可以画出无数条无差异曲线，以致覆盖整个平面坐标图。同一条无差异曲线上的不同点所代表的不同消费组合给消费者带来相同的效用，不同的无差异曲线上不同消费组合给消费者带来不同的效用。所有这些无差异曲线之间的相互关系是：离原点越远的无差异曲线代表的效用水平越高，离原点越近的无差异曲线代表的效用水平越低。在图6－4中，I1、I2、I3是三条不同的无差异曲线，它们分别代表不同的效用水平，其效用大小为I1>I2>I3。

（3）在同一坐标平面图上的任何两条无差异曲线不会相交。这一点可以用图6－5来说明。

图6－4　不同效用的无差异曲线

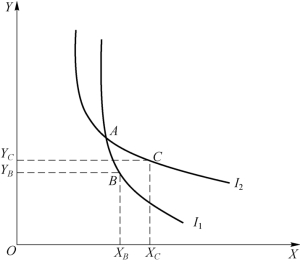
图6－5　两条无差异曲线相交

在图6－5中，两条无差异曲线相交于点A，这种画法是错误的。其理由在于：根据无差异曲线的定义，由无差异曲线I1可得点A、点B的效用水平是相等的，由无差异曲线I2可得点A、点C的效用水平是相等的。于是，根据偏好可传递性的假定，必定有点B和点C的效用水平是相等的。但是，观察和比较图中点B和点C的商品组合，可以发现点C的每一种商品的数量都多于点B，于是，根据偏好的非饱和性假定，必定有点C的效用水平大于点B的效用水平。这样一来，矛盾产生了：该消费者在认为点B和点C无差异的同时，又认为点C要优于点B，这就违背了偏好的完全性假定。由此证明：对于任何一个消费者来说，两条无差异曲线相交的画法是错误的。

（4）无差异曲线凸向原点。无差异曲线是凸向原点的。这就是说，无差异曲线不仅向右下方倾斜，即无差异曲线的斜率为负值，而且，无差异曲线是以凸向原点的形状向右下方倾斜的，即无差异曲线的斜率的绝对值是递减的。为什么无差异曲线具有凸向原点的特征呢？这取决于商品的边际替代率递减规律。商品的边际替代率是一个重要概念，将在下面进行讨论。