调节作用测试：强迫使用和任务复杂性

如果变量M的变化影响原因变量X对结果变量Y影响的大小和方向，则称变量M是调节变量X对变量Y影响效果的调节变量（Hayes，

2013)。

为了测试变量M在变量X和变量Y之间的调节作用，需要对以变量Y作为依靠变量，变量X、变量M以及变量X和M的乘积作为独立变量进行回归分析。如果变量X和M的乘积显著，则表明变量M是因变量X对结果变量Y影响的调节变量，即原因变量和结果变量的关系受到变量M的影响（Hayes，2013）。研究使用Hayes（2013）提供的SPSS计算软件包（Process）完成相应的数据分析工作。Hayes的Process软件包输出的调节效应分析结果如表3.6所示。

表3.6　调节作用和条件效应检验

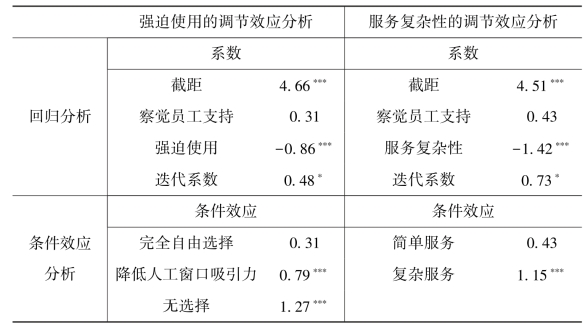
注：***P＜0.001；**P＜0.01；*P＜0.05。

如表3.6所示，两个回归方程结果都显示，迭代效应为正且显著，表明察觉员工支持对自我效能的影响不但受到强迫使用程度的调节（迭代系数＝0.48，P＜0.05），也受到服务复杂程度的调节（迭代系数＝0.73，P＜0.05）。

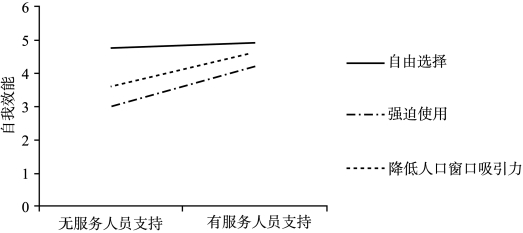
根据表3.6自动柜员机使用的强迫程度对自我效能影响的条件效应分析结果，在顾客被强迫使用自动柜员机的情况下，察觉员工支持对自我效能有着正向显著影响（effect＝1.27，P＜0.001）；在降低人工服务窗口吸引力情况下，察觉员工支持同样对自我效能有着正向显著影响（effect＝0.79，P＜0.001）；但是，顾客完全自由选择自动柜员机情况下，察觉员工支持对自我效能没有显著影响（effect＝0.31，P＞0.05）。以是否察觉到员工支持为横坐标，以自我效能为纵坐标，绘制不同强迫情境下自我效能水平的条件效果图，如图3.2所示：

(www.xing528.com)

图3.2 使用强迫性的调节作用分析

如图3.2所示，自由选择和强迫使用以及自由选择和降低人工窗口吸引力都不平行，按照条件效果图的图示特点（刘顺忠，2013），察觉服务员工支持和使用强迫程度之间存在明显的迭代效果。

回归迭代效应分析、条件效应分析和条件效果图分析都表明，察觉员工支持在强迫使用情况下对自我效能产生正向显著影响；而在顾客完全自由选择情况下对自我效能没有影响，研究假设2得到证明。

根据表3.6中使用自动柜员机完成任务复杂性对自我效能影响的条件效应分析结果，在复杂任务的情况下，察觉员工支持对自我效能有着正向显著影响（effect＝1.15，P＜0.001）；而在简单任务情况下，察觉员工支持对自我效能没有显著影响（effect＝0.43，P＞0.05）。以是否察觉到人员支持为横坐标，以自我效能为纵坐标，绘制不同任务复杂程度下自我效能水平的条件效果图，如图3.3所示。

如图3.3所示，简单任务和复杂任务不平行，按照条件效果图的图示特点（刘顺忠，2013），察觉服务员工支持和使用复杂性之间存在明显的迭代效果。

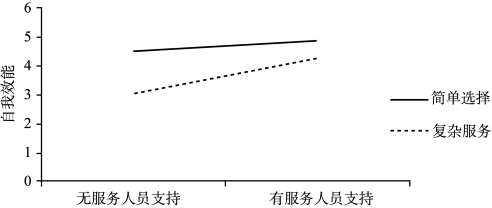
图3.3 服务复杂性的调节作用分析

回归迭代效应分析、条件效应分析和条件效果图分析都表明，察觉员工支持在复杂任务情况下对自我效能产生正向显著影响；而在简单任务情况下对自我效能没有影响，研究假设3得到证明。