生产要素的最优组合与成本——图解

最优的要素投入组合是指成本最小产量最大的组合，即用既定数量的成本生产最大产量的组合，或是用最小成本生产既定产量的组合。如把等产量曲线和等成本曲线放在同一坐标图上。那么，当这两条曲线相切时，切点所代表的组合就是要素投入的最优组合。

（一）既定成本条件下的最大产量

由于成本既定，所以只有一条等成本线C，既定的等成本线可以和许多等产量曲线相交，但只与一条等产量线相切，切点处所代表的组合是最优投入组合。

为什么只有在这个切点时才能实现生产要素的最适组合呢？

图4-11中，等成本线C与等产量曲线Q1相交于F点、G点，与等产量曲线Q2相切E点，与等产量曲线Q3不相交也不相切。这意味着，用成本C可生产低产量Q1，但太不经济；用成本C生产产量Q3根本不可能；用成本C生产Q2既可能，又最经济，故E点为生产者均衡点。

图4-11　既定成本下产量最大的要素组合

（二）既定产量条件下的最小成本

图4-12中，Q为等产量曲线，C1、C2、C3为三条等成本线，其中C3代表成本最大，C2次之，C1代表成本最低。图中等产量曲线Q与等成本线C3相交于F点、G点，与等成本线C2相切于E点，与等成本线C1不交不切。这意味着，用高成本C3可以生产产量Q，但是太不经济；用低成本C1生产产量Q根本不可能；用成本C2生产产量Q既是可能的，又是最经济的，故E点为生产者均衡点。(www.xing528.com)

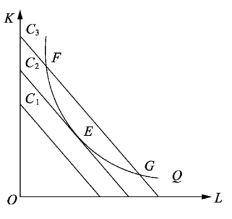
图4-12　既定产量下成本最小要素组合

无论是成本最少组合，或是产量最大组合，都是等产量曲线与等成本线切点的组合。

微观经济分析把上述等产量曲线与等成本线的切点E叫作生产者均衡点。在这一点上，生产者实现了用最小成本生产出最大产量，也就是达到了利润最大化。只要其他条件不变化，生产者就愿意继续保持这种状态。

在生产者均衡点上，等产量曲线的斜率正好等于等成本线的斜率。由于等产量线的斜率是两种生产要素的边际技术替代率（-ΔK／ΔL），等成本线的斜率是两种生产要素的价格比率（PL／PK）。所以：

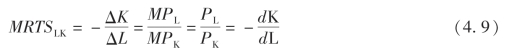
即边际技术替代率等于两要素的价格比。由此可得：

通常经济学家将（4.10）式称为生产者（或厂商）均衡条件，也叫最优要素组合的边际条件。也就是说，在生产者均衡条件下，生产者（或厂商）花费每一单位成本无论购买哪一种生产要素，获得的边际产量都相等。