第二章 人员招聘与配置
一、员工录用决策——补偿式 P94-95
各种项目的权重情况
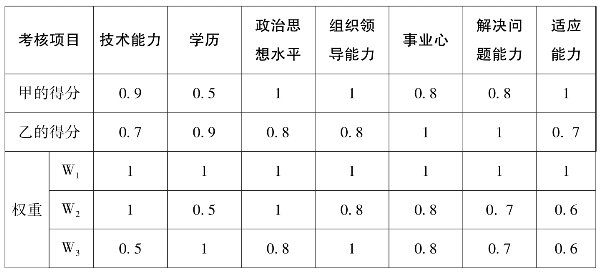
如:重视技术能力和政治思想水平,采取权重W2,即甲得4.75 分,乙得4.51分,甲为优,其他两种权重,计算方法一样,以此类推。
甲得分:0.9×1+0.5×0.5+1×1+1×0.8+0.8×0.8+0.8×0.7+1×0.6=4.75 分
乙得分:0.7×1+0.9×0.5+0.8×1+0.8×0.8+1×0.8+1×0.7+0.7×0.6=4.51 分
二、企业员工配置的基本方法 P113-114
表1 10 位应聘者在5 种岗位上的综合测试得分
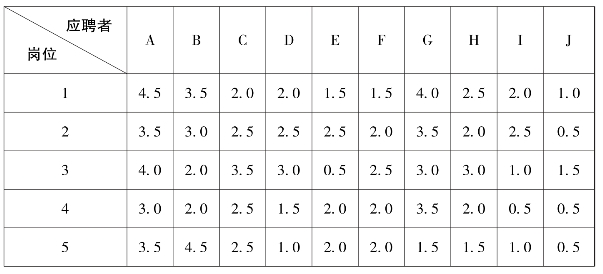
1.以人员为标准进行配置
即从人的角度,按每人得分最高的一项给其安排岗位,但这样做可能会出现同时多人在该岗位上的得分最高,结果只能选择一个员工,而使优秀人才被拒之门外。 由此可得:A (4.5)从事岗位1、E (2.5)或I 从事岗位2.C (3.5)从事岗位3.B (4.5)从事岗位5,岗位4 空缺,分数计为0。
根据表1 数据:
若考虑空缺岗位的影响,其录用人员的平均分数是:(4.5+4.5+3.5+2.5+0)/5 =3.0
若不考虑空缺岗位的影响,其录用人员的平均分数是:(4.5+4.5+3.5+2.5)/4 =3.75
2.以岗位为标准进行配置
即从岗位的角度出发,每个岗位都挑选最好的人来做,但这样可能会导致一个人同时被好几个岗位选中,尽管这样做的组织效率最高,但只能在允许岗位空缺的前提下才能实现,因此常常不可能的。 由此可得:岗位1 只能是由A (4.5)做(在岗位3 上A 的得分最高,但一人不能从事二职,因此岗位3 出现空缺),岗位2 或岗位4 由G (3.5)做,岗位5 由B(4.5)做。
根据表1 数据:
若考虑空缺岗位的影响,其录用人员的平均分数是:(4.5+4.5+3.5+0+0)/5 =2.5
若不考虑空缺岗位的影响,其录用人员的平均分数是:(4.5+4.5+3.5)/3 =4.17
3.以双向选择为标准进行配置
即在岗位和应聘者之间进行必要调整,以满足各个岗位人员配置的要求。 由此可得:岗位1 只能是由A (4.5)做,岗位2 由E (2.5)或I(2.5)做,岗位3 由C (3.5)做,岗位4 由G (3.5)做,岗位5 由B(4.5)做。
其录用人员的平均分数为(4.5+4.5+3.5+3.5+2.5)/5 =3.7
二、员工任务的指派方法(匈牙利法)P114-120
在应用匈牙利法,解决员工任务合理指派问题时,应当具备两个约束条件:
1.员工数目与任务数目相等;
2.求解的是最小化问题,如工作时间最小化、费用最小化。
(一)匈牙利法的应用实例
假定某单位有甲、乙、丙、丁、戊五个员工,需要在一定的生产技术任务组织条件下,完成A、B、C、D、E 五项任务,各个员工完成每项工作所需要耗费的工作时间见下表:
各员工完成任务时间汇总表
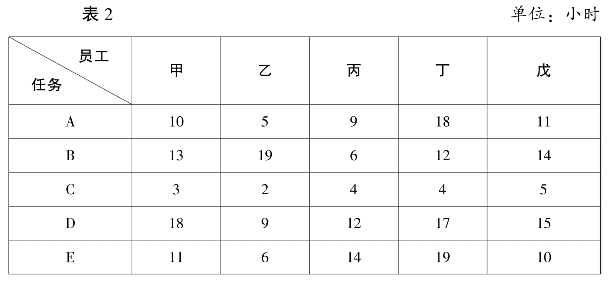
求解:员工与任务之间应当如何进行配置,才能保证完成工作任务的时间最短?
1.根据表2 数据,以各员工完成各任务的时间构造矩阵一:
矩阵一

2.对矩阵一进行行约减,即每一行数据减去本行数据中的最小数,得矩阵二:
矩阵二

3.检查矩阵二,若矩阵二各行各列均有“0”,则跳过此步,否则进行列约减,即每一列数据减去本列数据中的最小数,得矩阵三:
矩阵三

注意:也可先进行列约减,再进行行约减。
4.画“盖0” 线。 即画最少的线将矩阵三中的“0” 全部覆盖,得矩阵四:
矩阵四
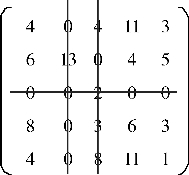
操作技巧:从含“0” 最多的行或列开始画盖“0” 线
5.数据转换。 若盖“0” 线的数目等于矩阵的维数则跳过此步; 若盖“0” 线的数目小于矩阵的维数(所谓维数,即几行几列,本例为五维,故要画5 条盖“0” 线)则进行数据转换,其操作步骤如下:
(1)找出未被盖“0” 线覆盖的数中的最小值λ,本例中的λ=1;
(2)将未被盖“0” 线覆盖住的数减去λ;
(3)将盖“0” 线交叉点的数加上λ。
本例结果见矩阵五,在矩阵五的数据上重复第4 步画盖“0” 线,盖“0” 线的数目没有等于矩阵维数,故重复第5 步进行数据转换得矩阵六。
矩阵五
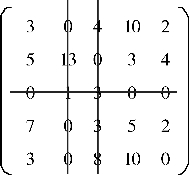
6.重复第4 步(盖“0” 线)和第5 步(数据转换),直到盖“0” 线的数目等于矩阵的维数,本例的矩阵五的λ=3。
矩阵六

7.求最优解。 对n 纬矩阵,找出不同行、不同列的n 个“0”,每个“0” 的位置代表一对配置关系。 具体步骤如下:
(1)先找只含一个“0” 的行(或列),将该行(或列)中的“0” 打“√”;
(2)将带有“√” 的“0” 所在的列(或行)中的“0” 打“×”;
(3)重复(1)步和(2)步至结束。 若所有的行列均含有多个“0”,则从“0” 的数目最少的行或列中任选一个“0” 打上“√”。(https://www.xing528.com)
其结果如下:
矩阵八
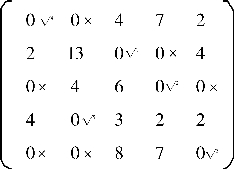
由上矩阵可见:甲负责任务A、乙负责任务D、丙负责任务B、丁负责任务C、戊负责任务E,这种配置才能用最短的时间完成所给任务。
(二)匈牙利法的推广应用 P118-120
1.员工数目与任务数目不一致的情况
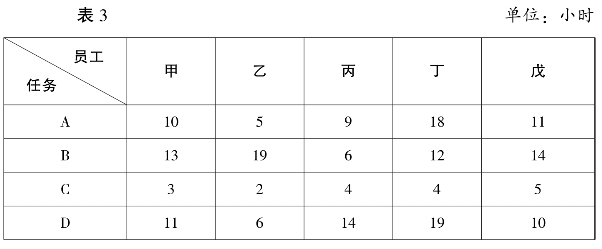
例如、乙公司目前有五名员工,需要完成四项任务,每名员工完成每项工作的工作时间见表3。
求解:应如何分配任务才能保证工作时间最短?
乙公司员工完成任务时间汇总表一
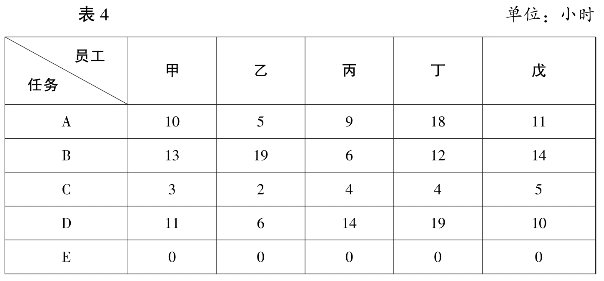
分析:五名员工负责四项任务,则必有一名员工没有任务,此时可增添一项虚任务E,则各员工完成任务E 的时间均为0,见表4。
乙公司员工完成任务时间汇总表二
此时,就可以用匈牙利法计算。
(三)当员工数目少于任务数目时,可让一名员工承担两项任务
例如,某公司安排两名员工完成三项任务,每名员工完成每项工作的时间见表5。
某公司员工完成任务时间汇总表
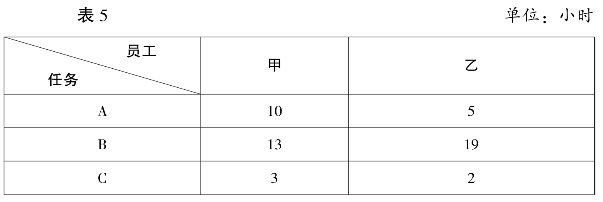
求解,应如何分配任务才能保证工作时间最短?
分析:两名员工负责三项任务,则必有一名员工须承担两项任务,因此增加甲′和乙′,分别表示他们完成第二项工作的情况,见表6。
某公司员工完成任务时间汇总表
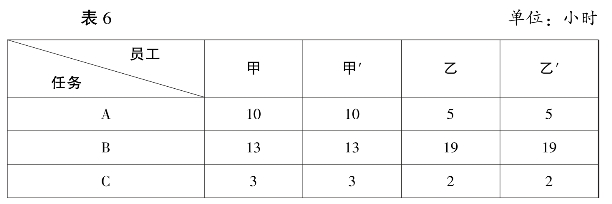
表6,员工数目多于任务数目,因此采用添加任务D,见表7。
某公司员工完成任务时间汇总表
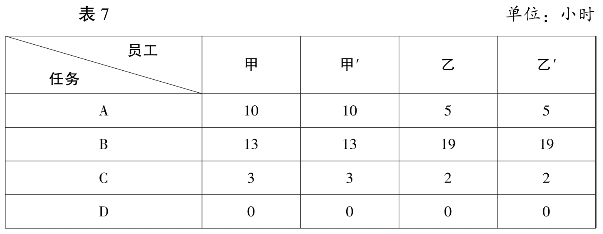
此时,就可以用匈牙利法计算。
(四)求最大化问题:
当所求问题为最大化值时,可用数据表中最大的数据分别减去数据表中所有数据,得出新的数据表,则问题转化为求最小值。
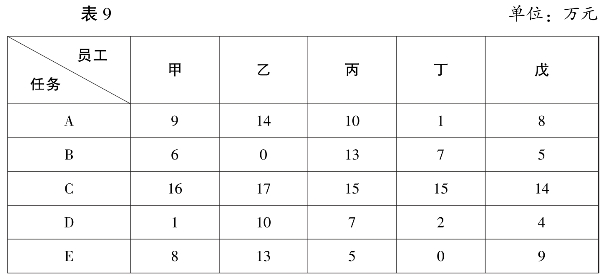
例如,丁公司目前有五名员工完成五项任务,每名员工完成各项任务所能获取的利润见表8。
丁公司员工完成任务收益汇总表
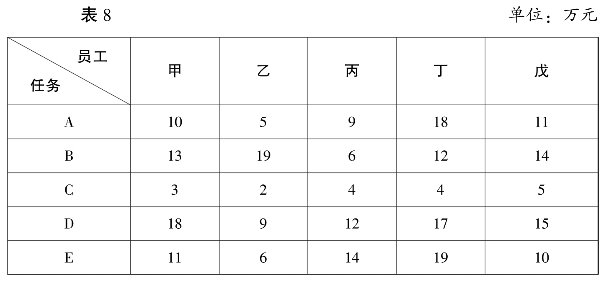
表8 中,最大的数据为19,用19 分别减去表中的各个数据,则数据表转化为表9,本题可用匈牙利法计算。
丁公司员工完成任务收益转换表
第五章 薪酬管理
(一)百分比系数法应用举例表 见表10 P327
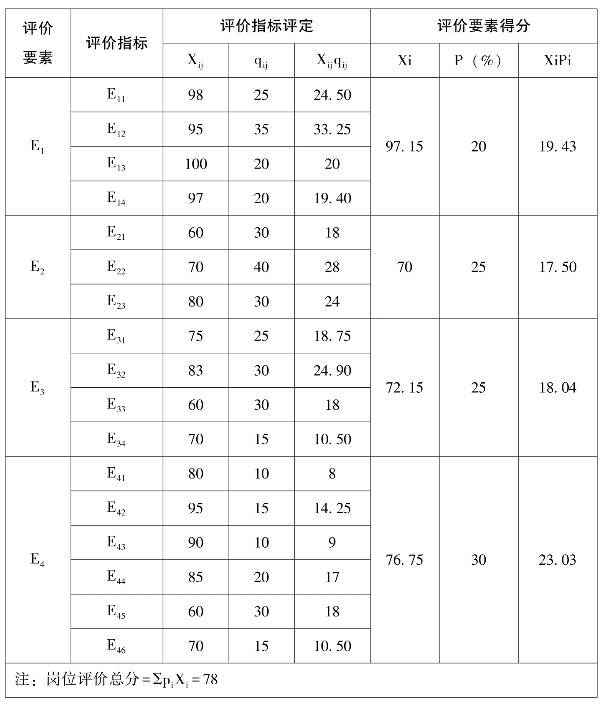
(二)权重系数的确定 P327
概率加权法
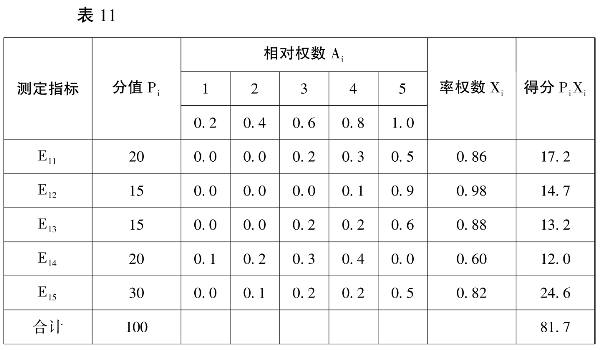
例如,指标E11的权数为
X1 =0.2×0.0+0.4×0.0+0.6×0.2+0.8×0.3+1.0×0.5 =0.86
P1X1 =20×0.86 =17.2
指标E12的权数为
X2 =0.2×0.0+0.4×0.0+0.6×0.0+0.8×0.1+1.0×0.9 =0.98
P2X2 =15×0.98 =14.7
指标E13的权数为
X3 =0.2×0.0+0.4×0.0+0.6×0.2+0.8×0.2+1.0×0.6 =0.88
P3X3 =15×0.88 =13.2
指标E14的权数为
X4 =0.2×0.1+0.4×0.2+0.6×0.3+0.8×0.4+1.0×0.0 =0.60
P4X4 =20×0.60 =12.0
指标E15的权数为
X5 =0.2×0.0+0.4×0.1+0.6×0.2+0.8×0.2+1.0×0.5 =0.82
P5X5 =30×0.82 =24.6
最后:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




