机制设计过程优化技巧

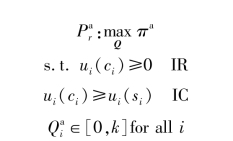
其中IR 是个人理性约束,该约束是为了确保每个供应商都会参与该采购机制;IC 是激励相容约束,该约束是为了确保每个供应商都会报出真实的成本。 和既往相关文献一样(如Chen,2007;Duenyas et al.,2013),定义供应商i(i =1,2)的虚拟价值为ψ(ci) =ci +F(ci)/f(ci),且设F 是对数凹的以确保ψ(ci)总是关于ci 单调递增(即正则性假设)。 通过求解上述规划,即得引理6.3。

引理6.3:在阶段1,若对于任意ci(i=1,2),订单分配规则Q 满足

则采购机制(Q,M)即为最优机制。

证明:采用和引理6.2 相同的分析过程,式(6.7)可化为

上述最优机制(Q,M)的实施过程如下:制造商需要先向供应商宣布如引理6.3所示的订单分配规则和支付规则,然后再请每个供应商报出自己的成本。 由于上述最优机制满足激励相容和个人理性约束,因此每个供应商的均衡策略是把自己的真实成本汇报给制造商。 最后,把他们的真实成本代入式(6.8)和式(6.9),便得到了每个供应商获得的订货数量和支付。

为方便表述,接下来用Q(i)和M(i)(i=1,2)分别表示成本为c(i)的供应商所获得的订货量和支付,其中c(1),c(2)(c(1) ＜c(2))是c1,c2 的顺序统计量。 在此基础上,即得引理6.3 的显式解。

引理6.4:在阶段1,成本为c(i)的供应商获得的订货量为

相应的支付为

其中,

证明:式(6.8)可化为

(www.xing528.com)

其中,Q=[Q(1),Q(2)]。 令

和对称信息相比,引理6.4 表明在不对称信息下,成本为c(i)(i =1,2)的供应商可以获得额外支付Δ(i),它本质上就是制造商为确保供应商i 报出自己的真实价值c(i)而支付的信息租金。 推论6.1 给出了产能约束k 对信息租金Δ(i)的影响。

表6.3　不对称信息下制造商的最优推式订货决策

注:。

证明:根据机制设计理论(Myerson,1981;Krishna,2009),最优机制必满足

其中,c=(c(1),c(2))且z(c)是(c(1),c(2))的联合密度函数。 根据引理6.4,上式可改写为

即

且制造商的最优期望利润为