原始设备制造商和集成制造商数量决策的优化方案

接下来分析制造商M1 的常规采购数量(Qr)决策,以及制造商M2 的投产数量(Q2)决策,其中M1 和M2 的决策同时进行。

给定M2 的投产数量Q2,M1 需决策常规采购数量Qr 以最大化自己的期望利润:

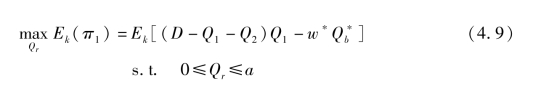
其中,Q1 =Q0 +Q∗

b ,Q0 =min(k,Qr)。

解上述规划,得引理4.3。

引理4.3:给定制造商M2 的投产数量Q2,制造商M1 常规采购时的最适反应函数为

证明:由于Q0 =min(k,Qr),根据表4.2 可得表4.3。

表4.3　w∗和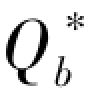 的值

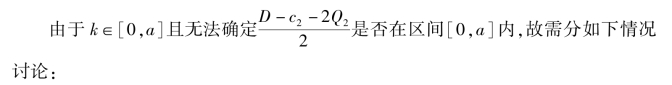
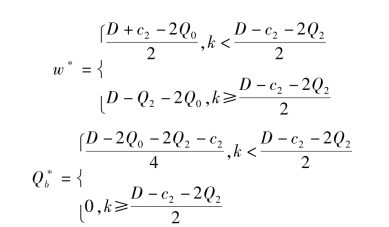
此时(4.9)式的目标函数可进行如下化简:

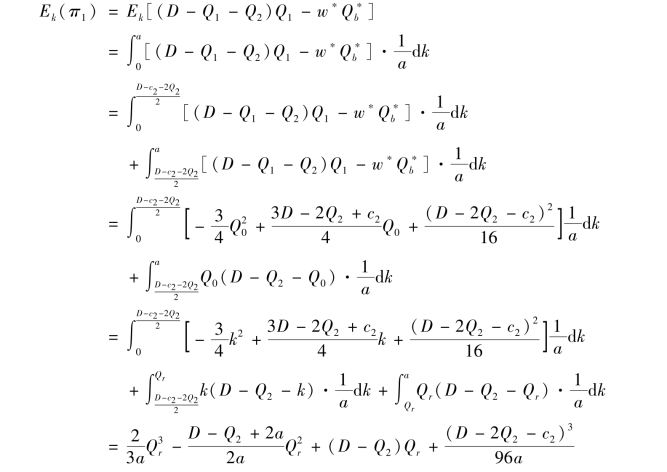
结合①和②可得

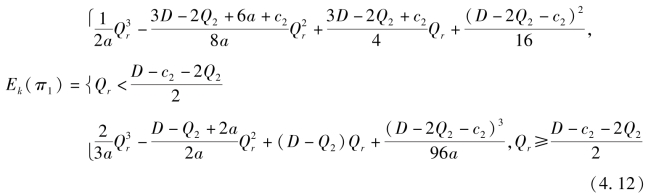
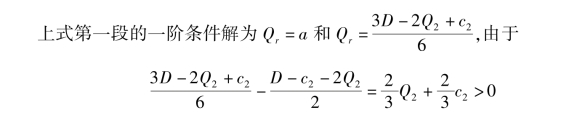
因此Ek(π1)的第一段总是关于Qr 单调递增。 Ek(π1)的第二段的一阶条件解为

即

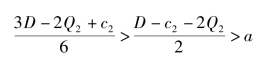
因此式(4.13)的最优解为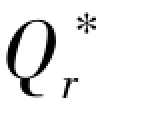=a。

综上,

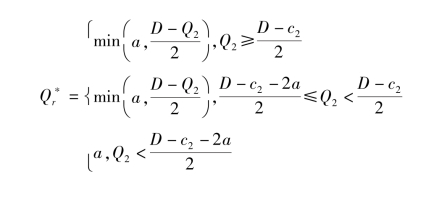
不难发现,上式可进一步化简为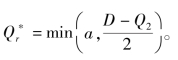证毕。

给定制造商M1 的常规采购数量Qr,制造商M2 需决策投产数量Q2 以最大化自己的期望利润:

其中,Q1 =Q0 +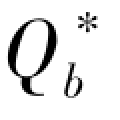,Q0 =min(k,Qr)。(www.xing528.com)

解上述规划,得引理4.4。

引理4.4:给定制造商M1 的常规采购数量Qr,制造商M2 在决策投产数量时的最适反应函数为

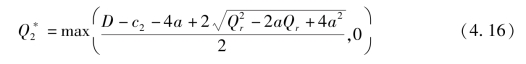
证明:由于Q0 =min(k,Qr),根据表4.1 可得表4.4。

表4.4　w∗和的值

此时式(4.14)的目标函数可进行如下化简:

此时和式(4.17)一样,式(4.14)的目标函数可化为

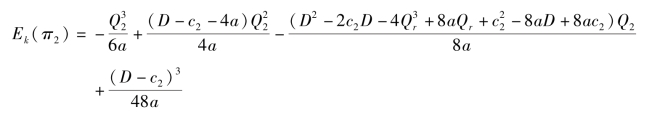
结合①和②可得

且

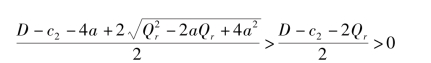
因此式(4.18)在

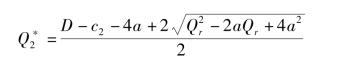
处取得最大值。

综上,

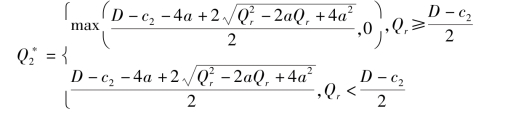
上式可化为

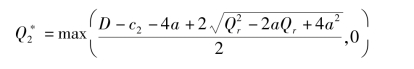
证毕。

根据引理4.3 和4.4,即得命题4.2。

命题4.2:制造商M1 的最优常规采购数量决策和制造商M2 的最优投产数量决策如表4.5 所示。

表4.5　制造商M1 和M2 的最优决策

证明:联立求解式(4.10)和式(4.16),即得命题4.2。 证毕。

命题4.2 表明,由于制造商M1 在常规采购时具有成本优势(c1 ＜c2),因此其常规采购数量总是大于0(＞0)。 但是,M1 的常规采购数量会受供应商产能可靠性的约束——常规采购数量必须小于供应商随机产能的上限值a。 命题4.2 还表明,当制造商M2 的成本较高且M1 的可靠性较高时,M2 在竞争中劣势明显,于是M2 会被对手挤出市场(即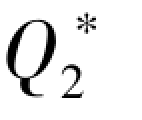=0)。 然而此时M2 的利润不一定为0,因为M2还可以在供应商S 的随机产能风险实现之后为M1 提供补货,并从中获利。