无代发货策略时的后备采购决策分析

在本节中,考虑零售商使用后备采购策略但不使用代发货策略的情形(情形三)。 此时,制造商需决策批发单价,零售商需决策常规采购数量和后备采购数量。

采用逆向归纳法,先分析零售商的后备采购决策。 给定制造商的批发单价w3(下标中的3 是情形三的标签,下同),零售商的常规采购数量Qr3,制造商实现后的供货成功率δ,零售商需决策一个后备采购数量Qb3以最大化其此时的利润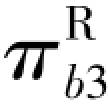,即

其中,p·min(D,Qb3 +δQr3)是零售商的收益,w3δQr3是常规采购成本,rQb3是后备采购成本,cl·min(D,Qb3 +δQr3)是发货成本。

接下来分析零售商的常规采购决策。 给定制造商的批发单价w3,零售商需决策一个常规采购数量Qr3以最大化其期望利润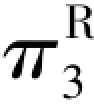,即

其中,ED[p·min(D,Qb3 +Qr3) -w3Qr3 -rQb3 -cl·min(D,Qb3 +Qr3)]是δ=1 时零售商的利润,ED[p·min(D,Qb3) -rQb3 -cl·min(D,Qb3)]是δ =0 时零售商的利润。

最后分析制造商的批发单价决策。 制造商只需决策一个批发单价w3 以最大化其期望利润,即

其中,aw3Qr3是制造商的期望收益,cQr3 是制造商的生产成本,aclQr3 是制造商将产品发送给零售所产生的期望物流成本。

解上述规划,可得引理3.3。

引理3.3:在使用后备采购货策略而不使用代发货策略的情形下(情形三),制

造商最优的批发单价为

零售商最优的常规采购数量为

零售商最优的后备采购数量为

证明:先解式(3.13)所在的规划。 由于实现后的δ 可能等于0,也可能等于1,因此分如下两种情况讨论:

(1)当δ=0 时,式(3.13)的目标函数可化为(www.xing528.com)

(2)同理,当δ=1 时,式(3.13)的目标函数可化为

综上,零售商最优的后备采购决策为

将上式第一段代入式(3.15)第一项,第二段代入式(3.15)第二项,并化简得

综上,零售商最优的常规采购决策为

将上式代入式(3.16)并化简得

综上,制造商最优的批发单价决策为

结合式(3.17)、式(3.19)和式(3.21),即得引理3.3。 证毕。

引理3.3 表明,在情形三中(即零售商只使用后备采购策略时),即便当制造商的批发单价和零售商的后备采购成本相同即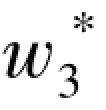 =r 时,零售商也会向制造商订货。这是因为,此时零售商实施常规采购和实施后备采购对利润的影响是无差异的,但是为了维护和制造商之间的长期合作关系,零售商还是更倾向于向制造商订货。而且,即使常规采购的订单最终没有送达(即发生供应中断),零售商依然能以r 的单位成本实施后备采购。

推论3.2:和情形一(即零售商既不使用代发货策略也不使用后备采购策略时)相比,后备采购策略的引入使制造商的批发单价降低^[1]即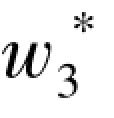≤w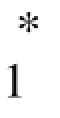,使零售商的常规采购数量增加即 ≥。

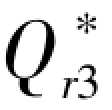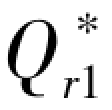证明:结合引理3.1 和引理3.3 可得

众所周知,后备采购策略具有应对供应中断风险的作用。 然而有趣的是,推论3.2 表明后备采购策略还有降低主供应商批发单价的作用。 这是因为,零售商后备采购的单位成本为r,这就迫使制造商的批发单价不能高于r,否则零售商将放弃常规采购而直接实施后备采购。 因此,后备采购策略的引入相当于零售商给制造商引入了一个竞争对手,于是制造商被迫降低批发单价,零售商相应地提高常规采购数量。

结合式(3.17)、式(3.19)和式(3.21)以及引理3.3,可得在情形三中制造商的最优期望利润为

零售商的最优期望利润为