零件质量可控因素及实验研究分析

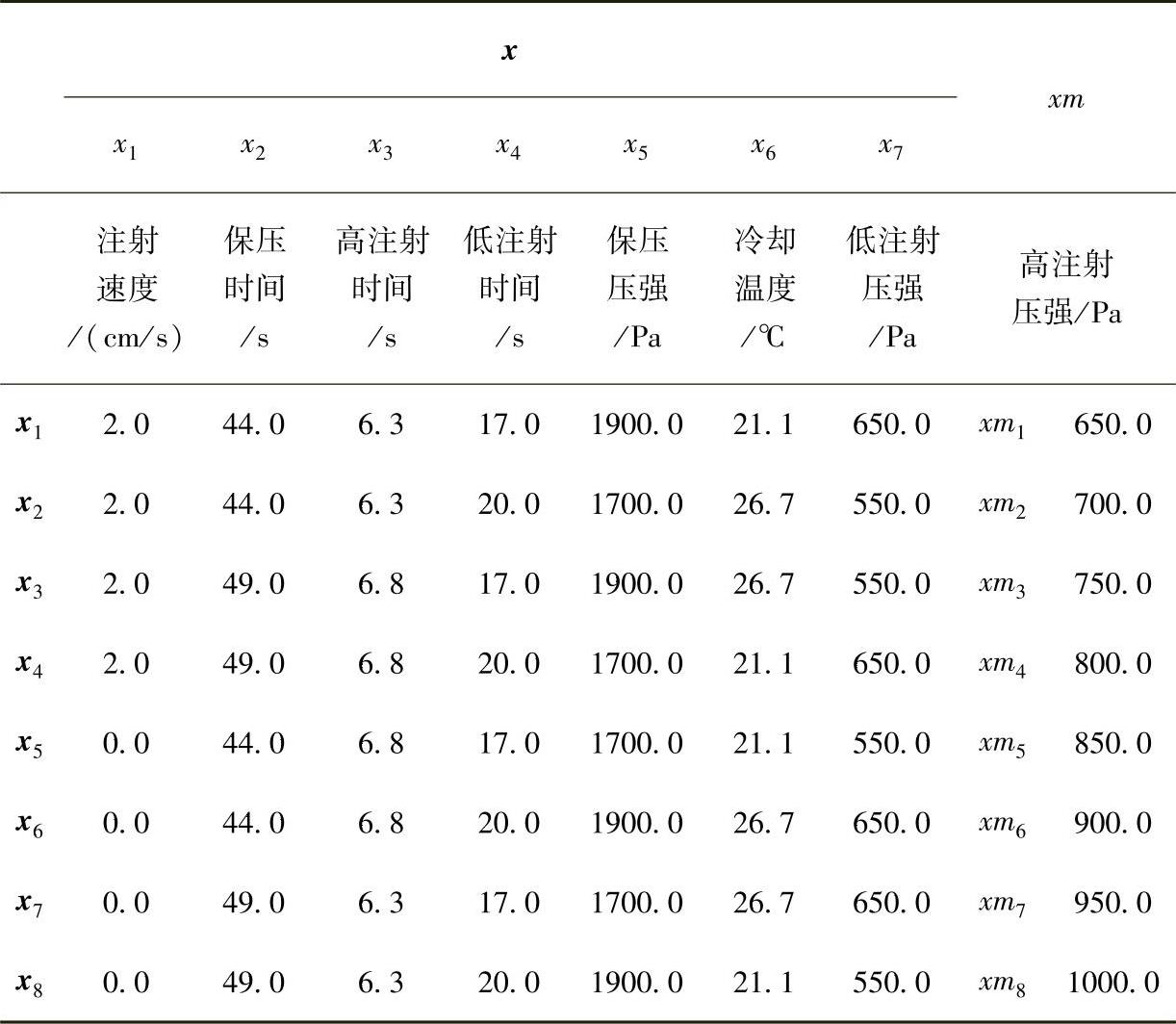
Jeff Wu在参考文献[155]报告过一个信号-响应系统的稳健性参数设计实例：在注射生产过程中，需要根据零件质量的要求注射不同量的高分子材料，因此需要一种能够动态控制材料注射量的可靠方法。由于高注射压强可以控制和改变材料的注射量，因此可将其看做信号因子xm，共有8个水平，分别为xm_i（i=1，2，…，8）。将零件质量看做响应变量y。可控因子有7个，分别是注射速度、保压时间、高注射时间、低注射时间、保压压强、冷却温度、低注射压强，形成可控因子的组合x=[x₁，x₂，…，x7]^T，其水平选择采用2^6-4析因设计，共有2^6-4=8个水平组合，即x_i（i=1，2，…，8），表6-1给出了可控因子组合及其8个水平的具体值、信号因子8个水平的具体值。噪声因子是由溶化指数、再研磨百分比、操作者、树脂湿度组合而成的综合因子，共有两个水平z₁和z₂，表6-2给出了y的实验数据。在每一个x_i处，对于每一个xm_i，分别在z₁和z₂处做4次重复。参考文献[155]利用响应函数建模方法对这一问题进行了分析。通过观察相关关系图，选择二阶多项式作为响应变量与信号因子的近似模型。根据析因实验结果，拟合出近似模型的系数β₀、β₁、β₂及方差σ²_p与可控因子之间的4个一阶多项式模型来反映响应变量与信号因子的变化关系

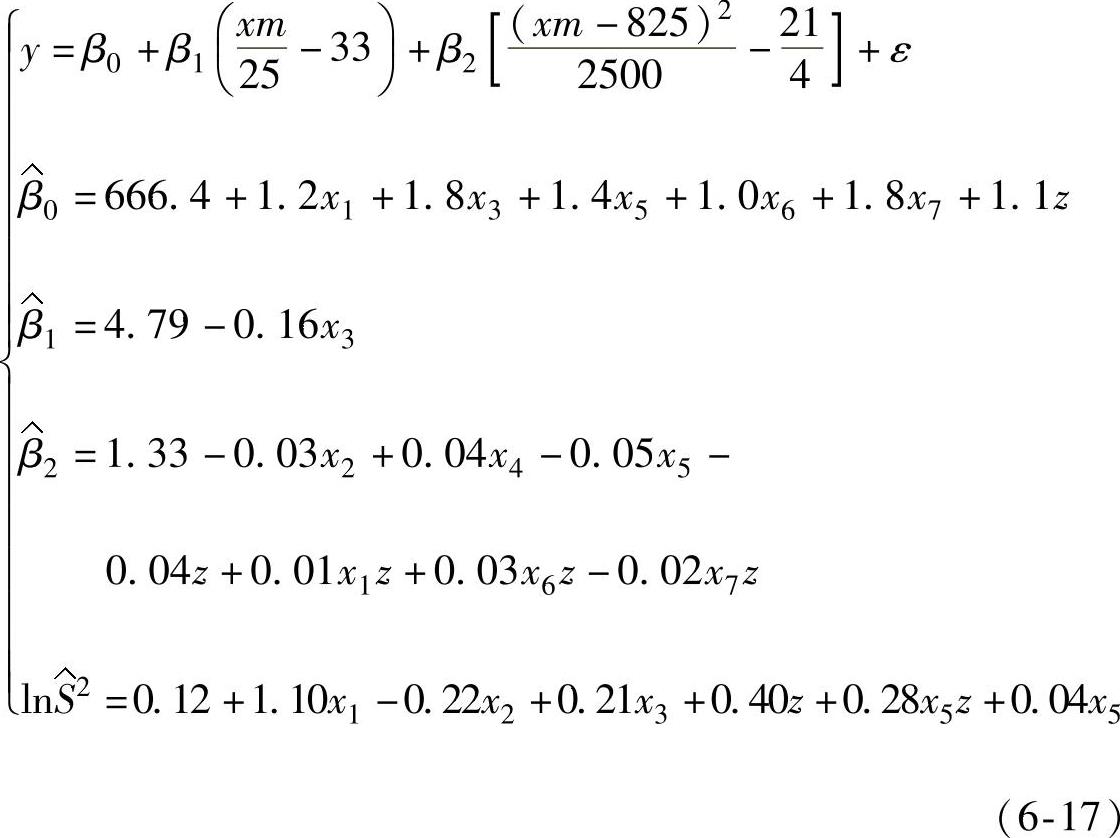
对上述4个一阶模型进行优化，其最终结果为：

但是由于该动态系统非线性相关的复杂性，在可控因子的某些组合处，二阶多项式会引起拟合不足，难以有效代表信号因子与响应变量之间相关关系的变化情况；此外，一阶多项式也不能真实地反映系数β₀、β₁、β₂及方差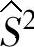关于可控因子的复杂作用关系情况，其优化结果仍有改善的空间。

表6-1 注射过程的可控因子组合及信号因子

注：数据来源：WU JEFF C F，MICHAEL H.试验设计与分析及参数优化[M].北京：中国统计出版社，2003.

表6-2 注射过程的实验数据(www.xing528.com)

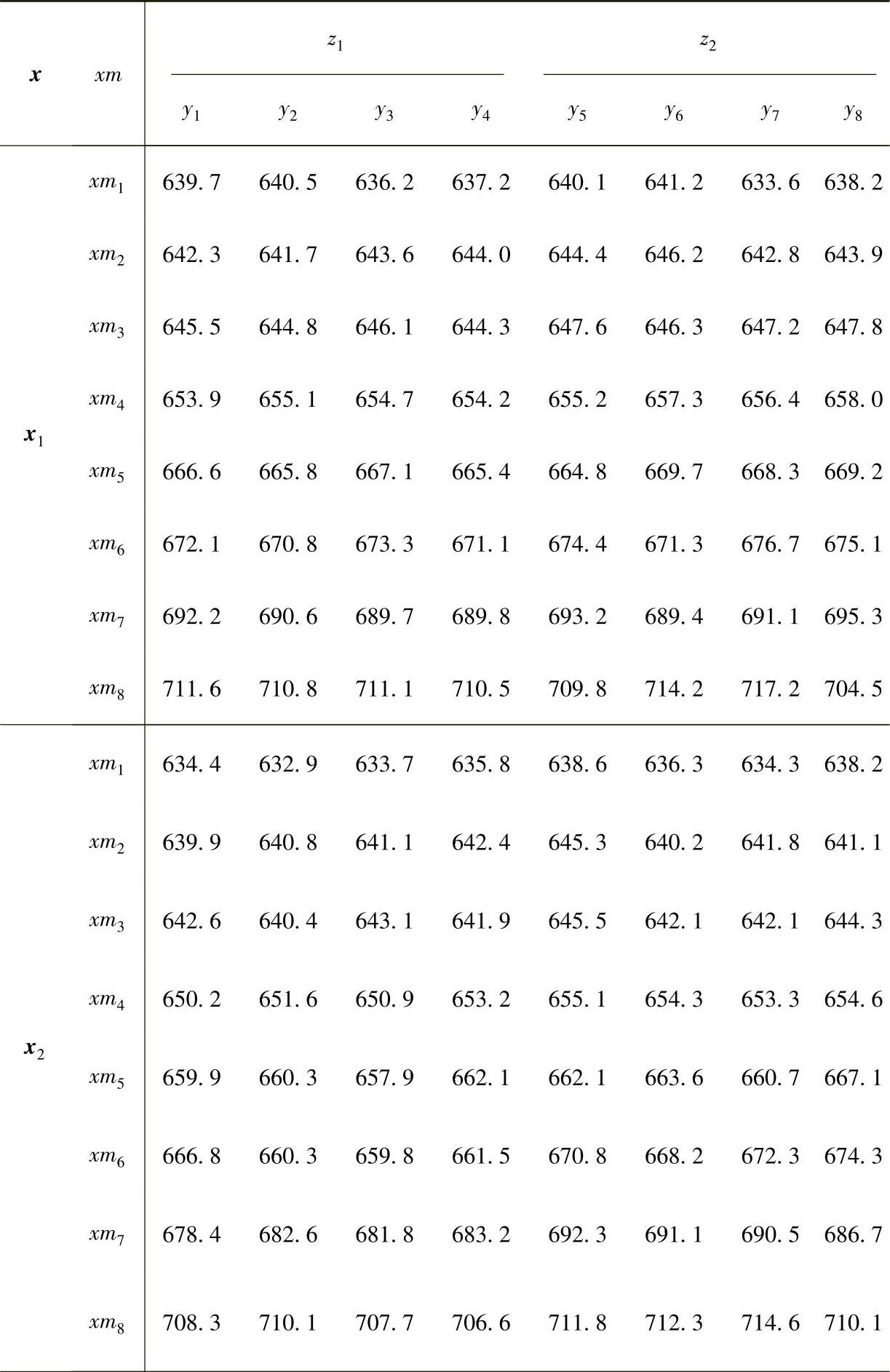
（续）

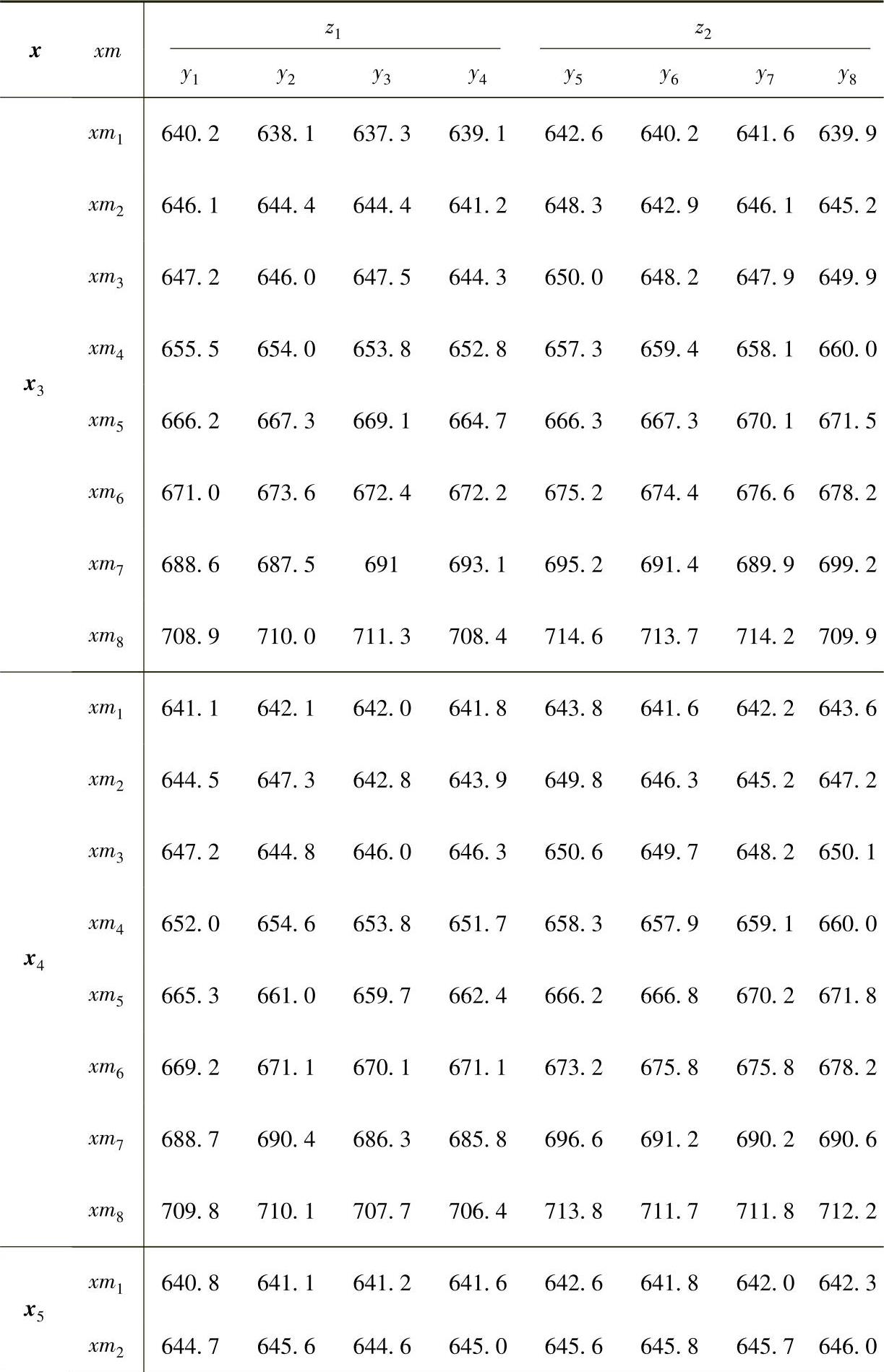
（续）

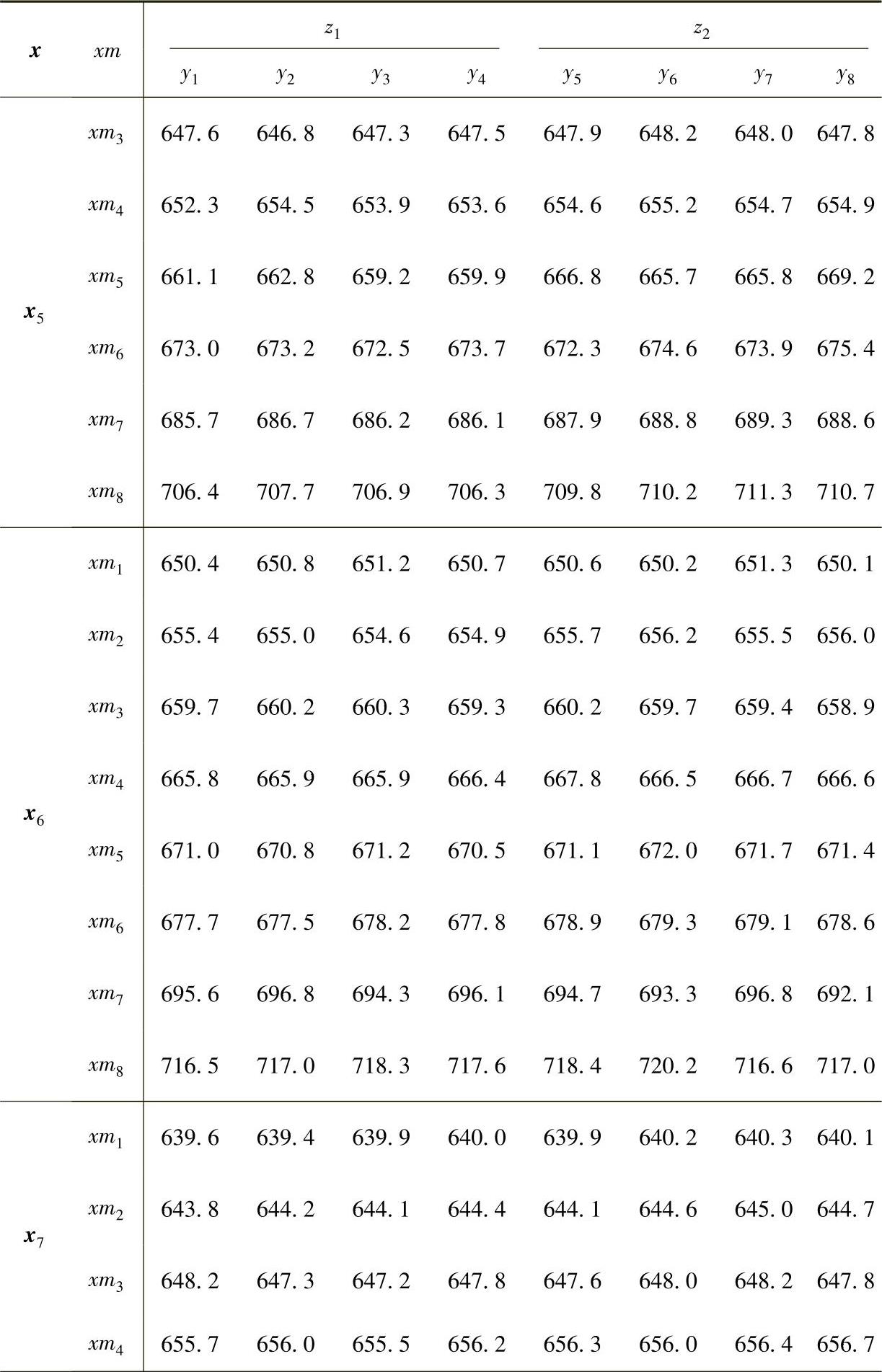
（续）

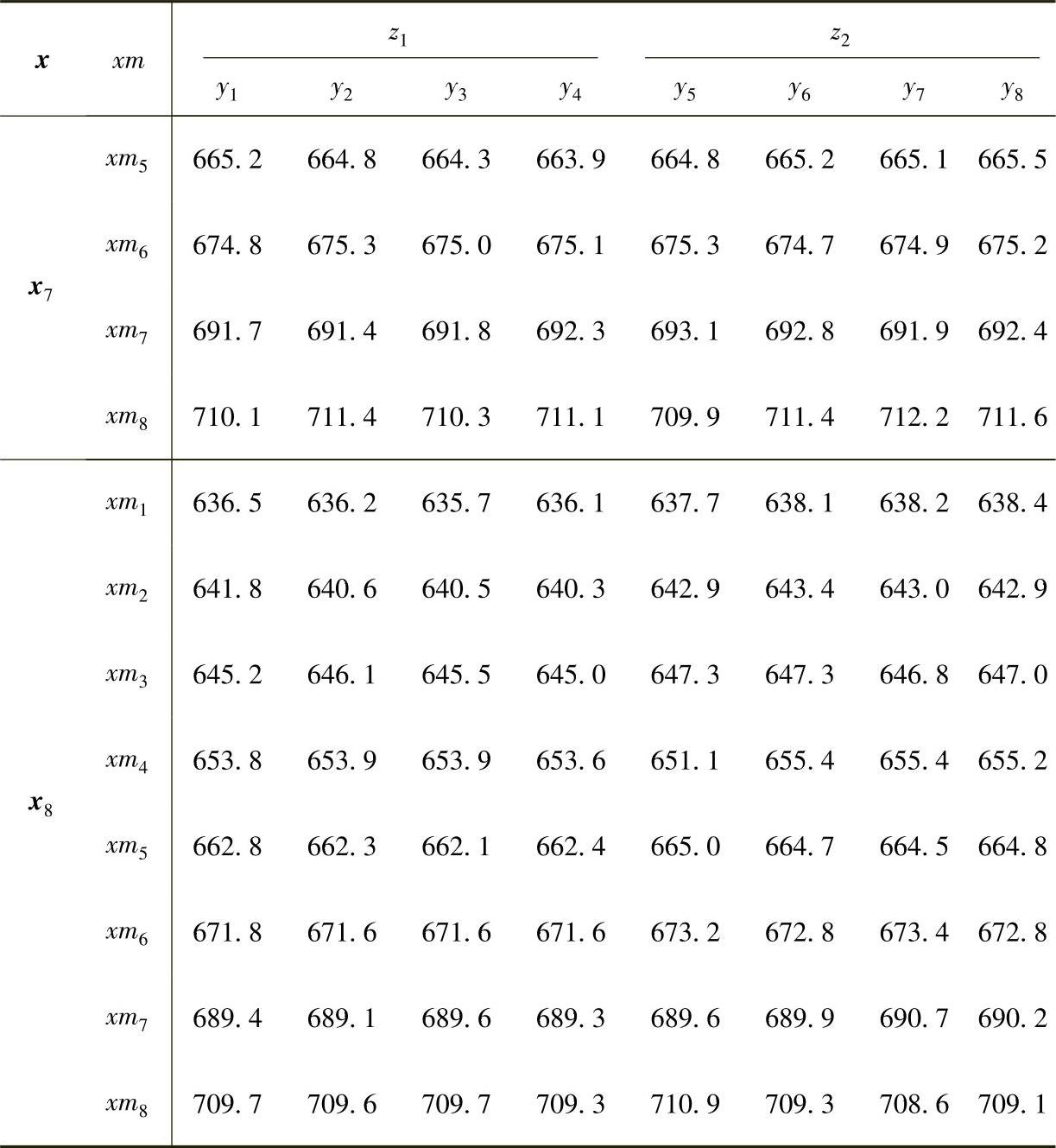
注：数据来源：WU JEFF C F，MICHAEL H.试验设计与分析及参数优化[M].北京：中国统计出版社，2003.