设动态系统由m个可控因子形成的可控因子组合记为x=[x1,x2,…,xm]T,其水平变化记为xi(i=1,2,…,p);由n个噪声因子形成的噪声因子组合记为z=[z1,z2,…,zn]T,其水平变化记为zj(j=1,2,…,q);有一个信号因子,记为xm,其水平变化记为xmk(k=1,2,…,r);y代表过程的响应变量。在上述分析的基础上,形成如下的基于支持向量回归机的非线性动态系统的稳健参数优化实现步骤:
(1)阶段1 寻找在不同信号因子情况下过程方差最小的可控因子组合。
步骤1:根据制造过程特点,选择合适的可控因子组合、噪声因子组合、信号因子的水平数p、q、r,采用经典实验设计、空间填充设计等方法,获取建模所需的样本集S0
S0={(xi,zj,xmk,yijk)|i=1,2,…,p;j=1,2,…,q;k=1,2,…,r}
(6-7)
式中 yijk——可控因子组合、噪声因子组合、信号因子不同的水平处的响应变量值。
步骤2:对于每一个可控因子组合的水平xi,将噪声因子组合的水平zj的变化看做重复,计算信号因子各水平xmk处的响应变量的方差Sik
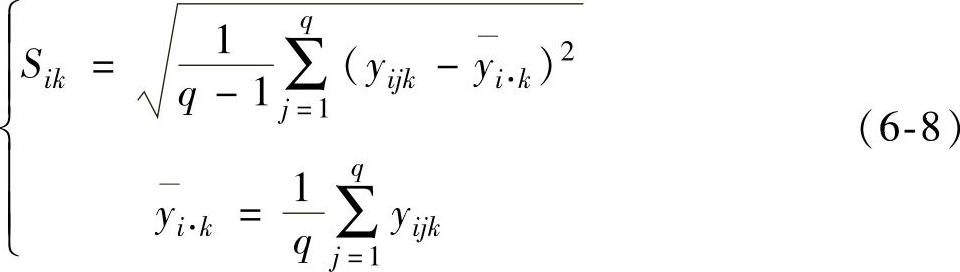
并进一步得到该可控因子水平处Sik的均值Si及方差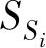
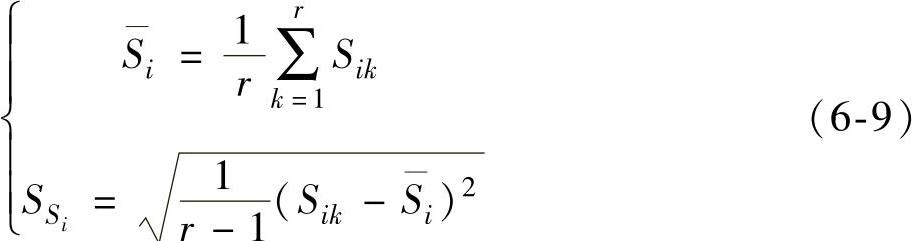
步骤3:形成第一阶段的样本集S1
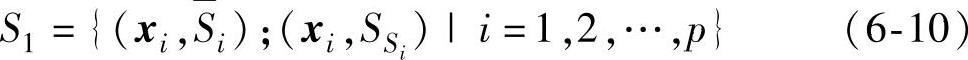
分别拟合 、SS关于x的方程SVR11与SVR12
、SS关于x的方程SVR11与SVR12
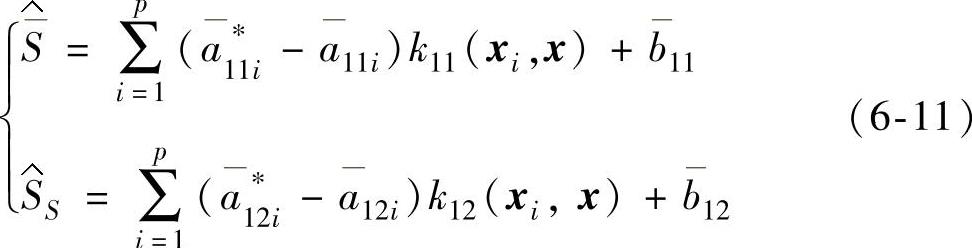
其中支持向量回归机模型参数的选择采用参考文献[152]中的方法。
步骤4:计算过程方差(即两类方差的总和)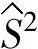
 (https://www.xing528.com)
(https://www.xing528.com)
以最小化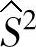 为目标和适应度函数,利用遗传算法对式(6-12)进行全局性寻优,得到最优解x∗与
为目标和适应度函数,利用遗传算法对式(6-12)进行全局性寻优,得到最优解x∗与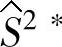 ,即可最小化过程方差。
,即可最小化过程方差。
(2)阶段2 拟合可控因子、信号因子与响应变量之间的作用关系模型。
将噪声因子看做重复,根据S0计算在可控因子组合及信号因子不同水平处响应变量均值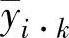 ,并由此形成第二阶段的样本集S2
,并由此形成第二阶段的样本集S2

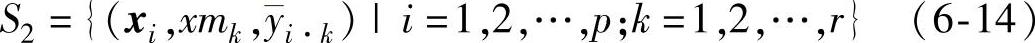
步骤5:令xm=x⊗xm代表可控因子组合与信号因子的所有水平组合,根据S2,利用支持向量回归机建立x、xm与y之间的近似模型SVR2
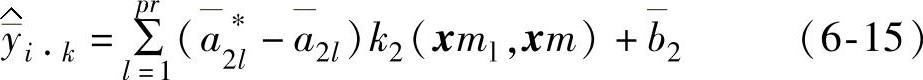
(3)阶段3 拟合信号因子与响应之间的非线性关系。
步骤6:将步骤4得到的x∗与信号因子水平形成新的因子组合x∗m=x∗⊗xm,代入模型SVR2即式(6-15),进行预测得到r个 ,其中“∗”代表可控因子的最优组合。由此得到第三阶段的样本集S3
,其中“∗”代表可控因子的最优组合。由此得到第三阶段的样本集S3
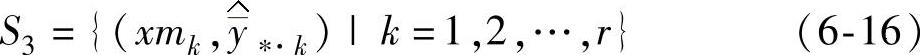
步骤7:根据S3作出xmk与 的相关图,选择合适的模型形式,拟合出具体的响应变量与信号因子间的作用关系模型,指导制造过程的生产实践和应用。
的相关图,选择合适的模型形式,拟合出具体的响应变量与信号因子间的作用关系模型,指导制造过程的生产实践和应用。
根据基动态系统的稳健性优化实现步骤,得到该算法的流程图如图6-3所示。
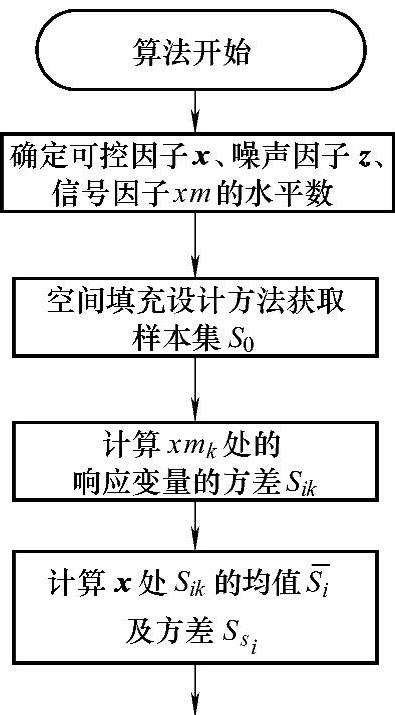
图6-3 基于支持向量回归机的动态系统稳健性参数优化算法流程图
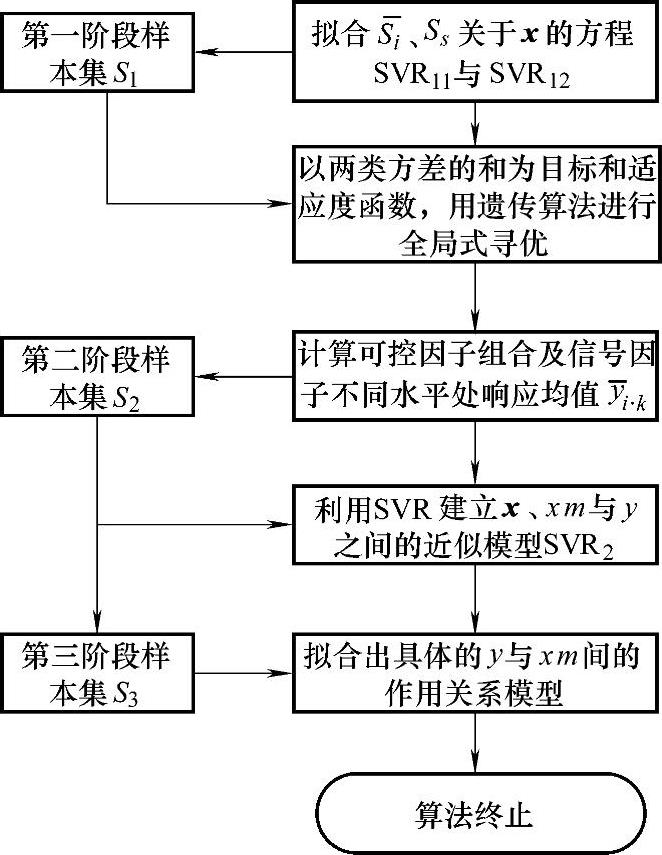
图6-3 基于支持向量回归机的动态系统稳健性参数优化算法流程图(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




