非线性动态系统的统计建模技巧

典型的信号-响应系统如图6-1所示。对于没有具体的物理或工程模型的制造过程，过程输出的质量特性（即响应变量）y受到三类因子的影响，即可控因子x、信号因子xm、噪声因子z。其中，xm与y之间存在一定的相关关系y=f（xm；x）+ε，该相关关系还要受到可控因子的影响，不同的可控因子水平，对应于不同的相关关系。z的存在使y在相同的xm、x水平时产生随机波动ε。对于线性的动态系统，响应变量y与信号因子xm之间的关系可用一元线性回归模型

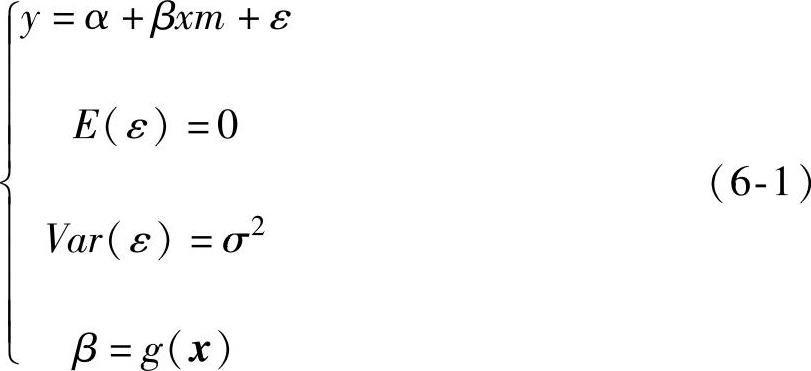
而非线性的动态系统则不能简单地用该模型表示，模型中有可能存在xm²、xm³等高阶项，甚至存在e^xm等超越函数形式的项。此外，噪声因子带来的方差也可能是变化的，为简单起见，用下式表示

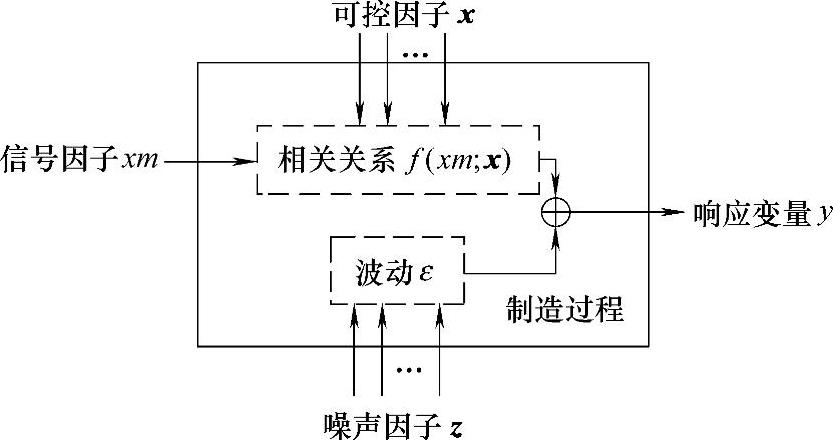
图6-1 典型的信号-响应系统

图6-2所示为信号-响应系统的线性和非线性相关关系示意图。(www.xing528.com)

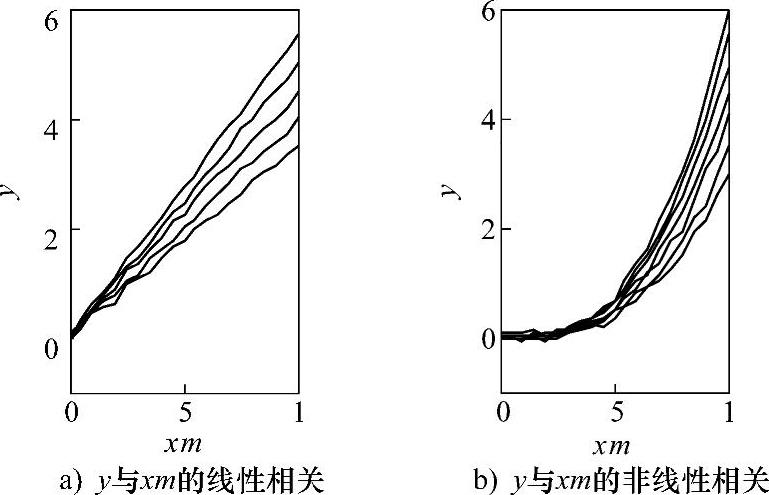
图6-2 信号-响应系统的线性和非线性相关关系示意图

对于线性的动态系统，Taguchi^[200]提出采用动态信噪比η=ln（β²/σ²）来考察过程的稳健性，首先利用正交实验和内外表设计对动态信噪比和灵敏度进行方差分析，确定稳健性最优的可控因子组合；而后再选择一个对β有影响而对η没有影响的调节因子，通过改变调节因子的水平使β达到目标值。该方法的原理较为简单，在实践中得到了较为广泛的应用，但是也存在明显不足：一方面，调节因子不一定总是存在；另一方面，该方法只能实现可控因子在特定实验水平上的优化，而不能实现连续优化。

为改进上述不足，Jeff Wu等^[155]学者提出了基于经典实验设计的响应函数建模方法，即采用析因试验、响应曲面设计等，对于可控因子（噪声因子）的第i个水平组合，拟合一条响应变量在信号水平上的回归线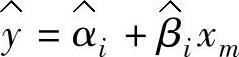，并估计出误差方差s²_i；在可控因子水平的变化范围内，分别拟合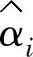、、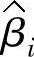lns²_i关于可控因子（噪声因子）的多项式回归模型，并由此评估过程的稳健性，确定最优的可控因子水平。进一步地，钟晓芳、刘思峰^[201]根据信号因子与响应之间的线性关系，利用灰色关联分析，选择与响应关联程度最大、波动最小的可控因子组合来实现稳健参数优化；汪建均、马义中^[202]利用联合广义线性模型，在区分显性和潜在噪声因子的基础上，通过调节信号-响应系统的截距α和斜率β来实现稳健参数优化；Pisvimol^[203]提出一种基于遗传算法和田口方法的动态系统的稳健参数优化实现方法；Jung和Yum^[57]为克服S/N指标的缺陷，利用人工神经网络建立了可控因子、噪声因子、信号因子与响应之间的近似模型，通过超拉丁方抽样估计β及其置信区间，进而求解约束优化问题使其波动最小；Chang和Chen^[204]利用人工神经网络和遗传算法，研究了多输出变量的动态系统的稳健参数优化问题；马义中、汪建均等^[205]研究了动态多响应系统的稳健性参数设计问题，提出一种基于满意度函数和灰色关联分析的实现方法。

上述研究对于动态系统稳健参数优化的理论及应用起到了较大促进作用，但是仍然存在需要继续深入之处：一方面，现有方法多适用于线性相关的动态系统，其主要步骤在于对式（6-1）中的参数α、β和σ²的估计和拟合，然而对于非线性相关来说，由于其关系形式远比式（6-1）复杂，而且过程方差也在发生变化，因而不能简单地用上述参数来表达；另一方面，随着制造过程的日益复杂化^[206]，响应函数建模方法中的多项式模型不足以反映可控因子、噪声因子、信号因子与响应变量之间的复杂作用关系；而人工神经网络模型虽然可以近似任意复杂的相关关系，但是需要较大的样本量，不适用于没有具体作用关系模型，且实验成本高、可获得样本量较小的制造过程的稳健性优化。因此需要研究新的实现方法。