1）本章将过程噪声的影响看做重复，并将响应变量的波动分为两部分，采用式（6-12）所示的过程方差来度量这两类波动，建立了过程方差与可控因子之间的支持向量回归机模型。而后以过程方差最小为目标，采用遗传算法对约束优化问题进行全局性寻优，得到了式（6-19）的可控因子的优化值，其对应的过程方差为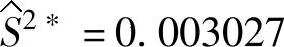
，与参考文献[155]响应建模方法的优化结果
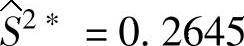相比，有较大程度改善，说明所提方法的整体性能较优。
2）从表6-3、表6-4可以看出，本章利用支持向量回归机建立的可控因子与过程方差之间的作用关系模型，其拟合效果较好（拟合
、SS的均方误差分别为0.0526和0.0234），因而可以较为真实地反映各类因子与过程方差之间的复杂作用关系。与之相比，响应建模方法采用多项式来拟合可控因子、噪声因子与过程方差之间的作用关系。从式（6-17）可以看出，该模型形式简单，易于优化，但是其最优值通常只能在可行域的端点处达到，不能实现真正意义上的连续优化。此外，模型中还含有噪声因子的一阶主效应项，在很大程度上影响到了过程方差估计的准确度。(www.xing528.com)
3）关于信号因子与响应变量的作用关系建模，本章所提方法对非线性相关关系的模型形式不做事先限定，在找到最优可控因子组合之后，才拟合具体的动态作用关系模型，其针对性强，适用性好；而表6-7的系数检验与方差分析结果也说明了模型的适合性。响应建模方法一开始即设定了二阶多项式模型的固定形式，然而在可控因子水平变化范围内，二阶多项式模型并不一定适用。对于本案例，参考文献[155]也指出，在16个可控因子组合的水平处，有4个水平处二阶多项式模型是不合适的，因此二阶模型的代表性不强。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
