基于支持向量回归机的双响应建模方法优化

这里以第四章的研究为基础，提出一种基于支持向量回归机的双响应建模策略，算法步骤如下：

步骤1：设μ_y和σ_y分别代表过程的均值和方差，以Lin和Tu^[174]提出的均方误差MSE作为最优化问题的目标函数。

MSE的定义为

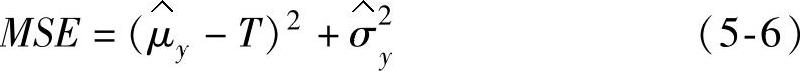
式中 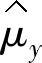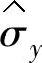，——μ_y和σ_y的估计值；

T——μ_y的目标值。

MSE综合考虑了过程μ_y和σ_y的影响，并且允许μ_y和目标T之间略有偏离，以得到较小的σ_y。

步骤2：求解最优化问题。

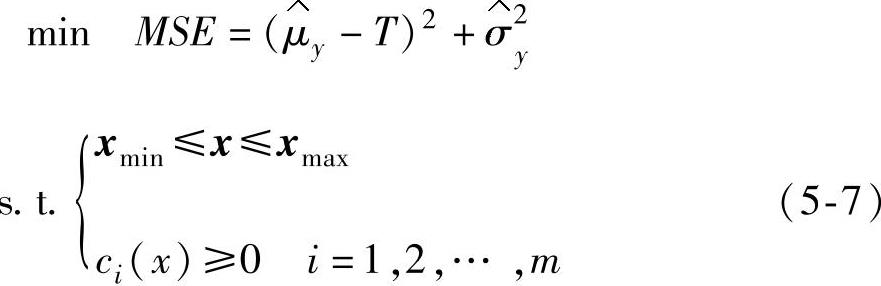
式中 x——过程可控因子组成的向量；

x_min，x_max——可控因子向量的下界和上界；

c_i（x）≥0（i=1，2，…，m）——可控因子之间的约束条件。

步骤3：MSE采用如下两种策略之一来计算。

设实验得到的样本集为：(www.xing528.com)

S={（x₁，y₁），（x₂，y₂），…，（x_l，y_l）} （5-8）

策略Ⅰ：利用支持向量回归机分别拟合过程的_μy和σ_y模型

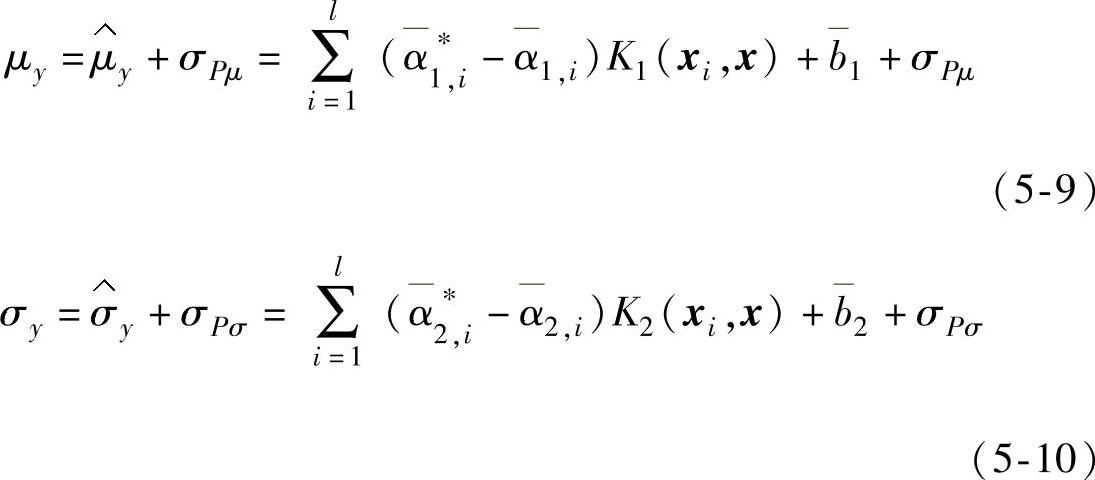
然后再计算式（5-7）中的MSE值。

策略Ⅱ：直接利用支持向量回归机拟合MSE模型

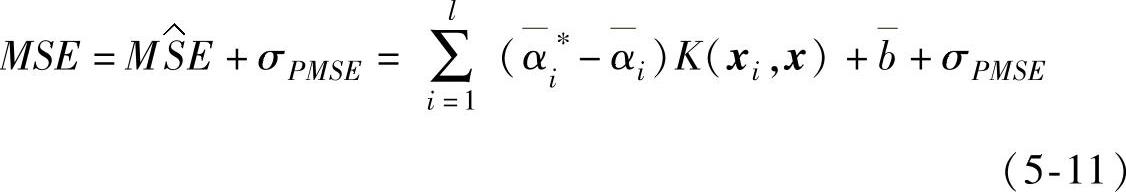
步骤4：样本集S采用乘积表（cross array）^[198]来获得。

设z代表过程的噪声因子组成的向量，在x的某一位级组合处，对z的所有位级组合进行实验（假设进行了n次实验），将这n次实验看做可控因子的n次重复，以此来计算在该可控因子的位级组合处，过程的均值、方差和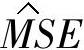的值。对可控因子的所有位级组合进行类似实验，就得到了拟合支持向量回归机方程所需的样本集。图5-1所示为两种策略的示意图。

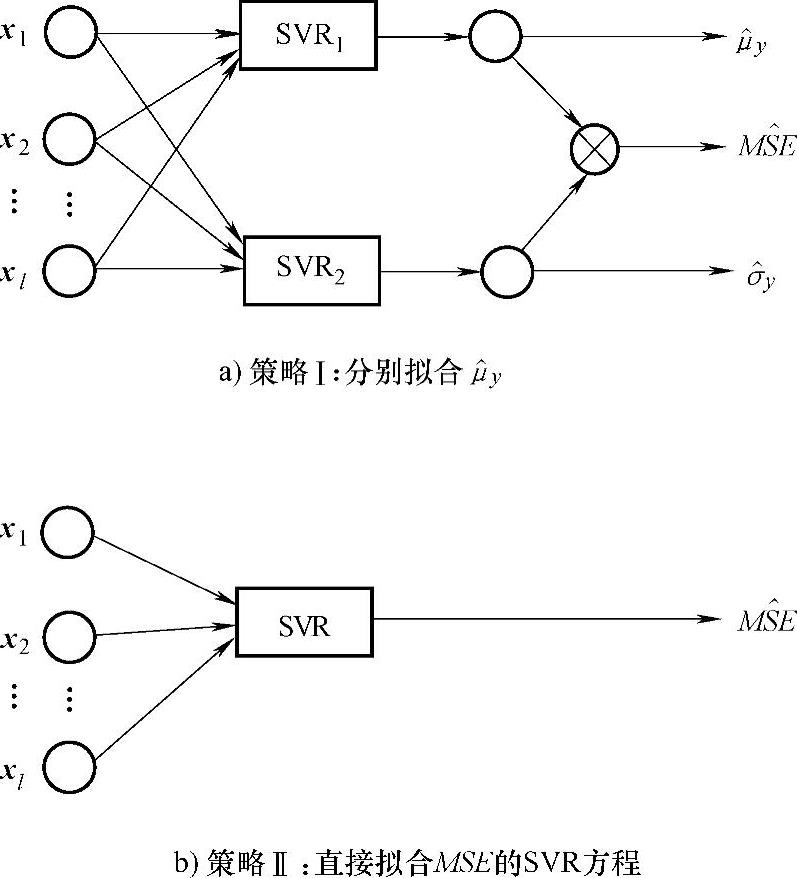
图5-1 基于SVR的DRSM的两种估计MSE的策略示意图

步骤5：对于策略Ⅰ和策略Ⅱ，分别以样本集S中的各样本点（x_i，y_i）（i=1，2，…，l）为寻优起点，并行运行序列二次规划算法以发现稳健性参数优化点。

基于支持向量回归机的双响应建模的算法流程图如图5-2所示。