如何利用响应曲面法进行质量优化？

对于上述质量优化和改进问题，由于没有真实的物理或工程模型，因此解决问题的关键在于能否通过某种方法建立过程的近似模型。该模型不仅应尽可能真实地描述影响因素与质量特性之间的关系，而且还应能进行预测和优化。由于对过程物理或工程机理的不了解，因此需要更多地从过程的实际运行表现中学习，通过现场实验得到输入与输出的数据样本集，利用统计学或数学方法建立拟合模型，并由过程的实际运行来验证和修正模型。

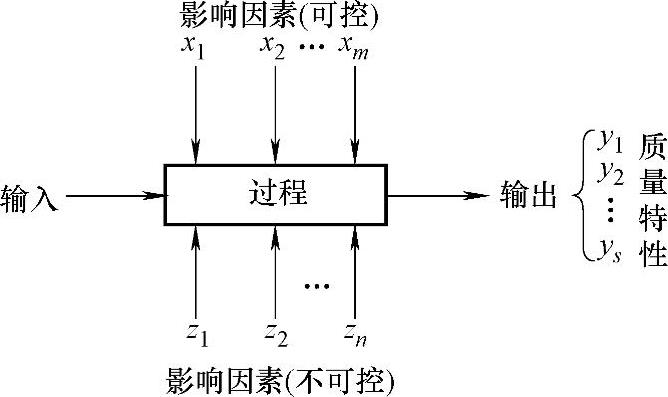
图4-1 影响质量特性的因素

基于上述思想，Box和Wilson^[153]于1951年提出了响应曲面法。响应曲面法是数学和统计方法结合的产物，它通过全因子设计、部分因子设计、中心复合设计等方法在工业生产条件下对过程进行实验，获取相关数据，并利用回归估计、方差分析、最速上升、正则分析等方法拟合与优化模型。响应曲面法是一套关于影响因素筛选、区域搜索、过程建模与优化的序贯性的实验设计方法和体系，为工程师与统计学家进行工业实验提供了一种全新的手段。Box指出，响应曲面法的实现构成了一个学习过程（learning process），并且可以归纳为“推测（conjecture）、设计（design）、实验（experiment）、分析（analysis）”四个基本步骤。而Myers^[126]又将响应曲面法分为实验设计、模型拟合、过程优化三方面的内容。半个多世纪以来，响应曲面法得到了极大的发展，成为了实验设计（Design of Experiment，DOE）^[154，155]的核心方法，其理论体系涵盖了稳健性方法、非参数方法、广义线性模型等新方法与技术，应用上则涉及了离散制造业、化学工业、食品与生物化学等诸多领域的质量改进及优化。

1.经典响应曲面法

响应曲面法将可以控制的影响因素x₁，x₂，…，x_m称为因子（factor），它们既可以是定量的，也可以是定性的，其中定量因子又分为连续型和离散型，因子的取值称为因子的位级或水平。y₁，y2，…，ys称为响应变量（response variables），过程也称为响应过程。设y是y₁，y₂，…，y_s中关心的某个响应变量，响应曲面法通过严格的实验设计和统计分析得到响应变量y关于因子的统计模型

y=f（x₁，x₂，…，x_m）+ε （4-1）然后根据模型进行分析，达到优化响应的目的。式（4-1）中f（x₁，x₂，…，xm）是某个确定的函数关系式；ε代表误差，包含不可控的影响因素及模型拟合不良而产生的误差，在经典响应曲面法中，一般认为ε～N（0，σ²），并且独立同分布（independ-ent identically distributed，i.i.d.）。于是，由式（4-1）可得y均值的估计

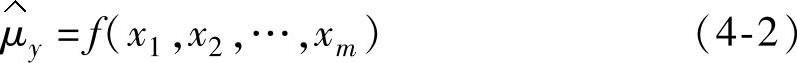
经典响应曲面法首先从一个特定的初始点开始，选择合适的因子位级，通过一个筛选实验（screening experiment）识别出y的主要影响因子，然后拟合如下形式的一阶多项式模型

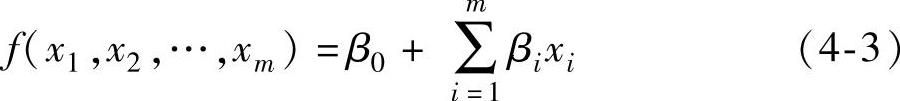
式中 β₀——截距项系数；

β_i——x_i的斜率或线性效应系数。

对模型进行统计分析，如果因子间的交互作用以及模型的曲度均不显著，则采用最速上升法（steepest ascent search）逐步进行实验。当观测到响应不再优化时重新拟合一阶模型，此时若模型的曲度显著，则通过添加实验点进行更为细致的二阶实验，拟合出如下的二阶多项式模型

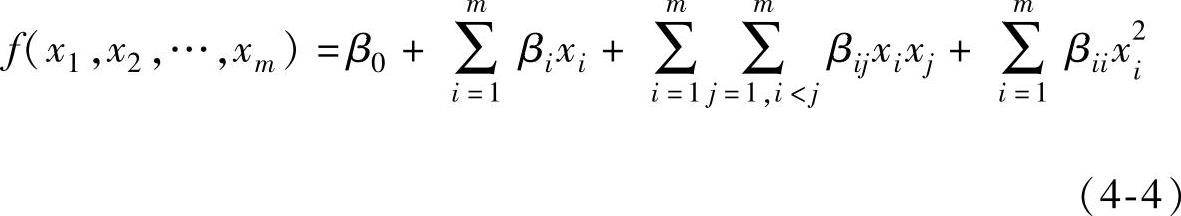
式中 β₀——截距项系数；

β_i——x_i的线性效应系数；

β_ij——x_i与x_j之间的线性×线性交互作用系数；

β_ii——x_i的二次效应系数。

如果模型的回归效应显著，拟合不良不显著，则认为在当前实验区域内二阶模型可以较好地近似响应与因子之间的关系，并进一步通过该模型对响应进行优化和预测，然后通过验证实验来验证结果的正确性。

拟合一阶模型可采用一阶设计（first order design），如全因子设计（full factor design）、部分因子设计（fractional factor de-sign）、Plackett-Burman设计等，并通过添加中心点来进行曲度检测。拟合二阶模型可采用中心复合设计（Central Composite De-sign，CCD）系列，如中心复合序贯设计（Central Composite Cir-cumscribed Design，CCC）、中心复合有界设计（Central Compos-ite Inscribed Design，CCI）、中心复合表面设计（Central Compos-ite Face-centered Design，CCF）、Box-Behnken设计、均匀外壳设计（uniform shell design）等。回归估计、方差分析是拟合以及分析一阶、二阶模型的主要方法；特别地，一阶、二阶模型中的系数均采用最小二乘法进行估计。对二阶模型进行优化时，令x=[x₁，x₂，…，x_m]^T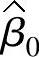，表示β₀的估计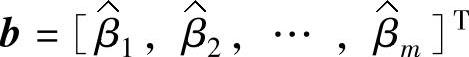，表示β₁，β2，…，βm的估计，表示式（4-4）中β_ij的估计矩阵，则二阶模型的估计方程如下

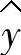对x求导并令其等于0，则有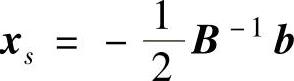，称其为式（4-5）的稳定点，将其代入式（4-5）得稳定点处的相应值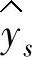，然后通过正则分析（canonical analysis）确定稳定点的类型，即最大值、最小值和鞍点。

2.基于广义线性模型的响应曲面法

经典响应曲面法假设过程服从正态分布，然而实际中常常会遇到非正态过程，例如单位产品缺陷点数的分布，可靠性分析中产品失效时间的分布等。为解决这一问题，研究者将广义线性模型引入到了响应曲面法。

正态线性模型有如下的形式

y=β₀+β₁x₁+β₂x₂+…+β_mx_m+ε （4-6）

式中 ε～N（0，σ²）。(www.xing528.com)

式（4-6）也可以将其等价地描述为y～N（μ_y，σ²），且

μ_y=β₀+β₁x₁+β₂x₂+…+β_mx_m （4-7）

广义线性模型将响应y的分布形式从正态推广到了指数形函数形式，例如Poisson分布、指数分布、Gamma分布、二项式分布等，其方程如下

η=β₀+β₁x₁+β₂x₂+…+β_mx_m=g（μ_y） （4-8）

式中 β₀，β₁，β₂，…，β_m——系数，采用极大似然法进行估计；

g（μ_y）——联系函数（link function），例如对于Poisson分布，g（μ_y）=lnμ_y，对于Gamma分布，g（μ_y）=μ_y^-1。

广义线性模型对响应的均值进行变换，变换后可以同时实现正态性、常数方差、线性性，优于通常采用的Box-Cox转换^[155]等。

Nelder和Wedderburn^[156]于1972年提出了广义线性模型，而后McCullough和Nelder^[157]、Myers和Montgomery等^[126]对广义线性模型进行了深入的研究。Lewis和Montgomery等^[158]指出对于响应均值的估计，广义线性模型的置信区间要比传统的最小二乘法短，说明广义线性模型估计的精度更高；Lee和Nelder^[159，160]系统地研究广义线性模型与稳健参数设计的关系，利用广义线性模型同时对均值和方差响应进行建模；Robinson和Wulff等^[130]提出一种广义线性混合模型（Generalized Linear Mixed Models，GLMM），并将其应用于响应为非正态而噪声因子为随机效应的半导体生产过程。

3.基于核函数回归与人工神经网络的非参数响应曲面法

经典响应曲面法以一阶、二阶多项式为模型，并假设过程服从正态分布，广义线性模型将过程的分布形式推广到了指数函数族，但从式（4-8）可以看出，它其实也是一种线性模型。这些模型均属于参数模型，即首先确定拟合方程的形式，然后通过实验估计方程的参数。但是实际中利用参数模型拟合常常会遇到困难，因为如果一开始就限制了模型的形式，则很有可能与实际情况不相符。例如对于双响应曲面中的方差响应，拟合所得到的可决系数R²往往较低^[137]，说明基于参数模型的响应曲面法并不适合于复杂的响应过程。

为此，研究者提出了非参数响应曲面法并进行了相关研究。Myers^[126]指出，对于需要寻找最优操作条件的响应过程，如果不关心拟合方程的具体解析形式而只关心它的描述能力，那么就可以应用非参数响应曲面法，而且拟合方程往往是高度非线性的。

与参数模型相比，非参数响应曲面法在拟合时并不限定模型的具体形式，只是假定其属于某类光滑函数，核函数回归（Ker-nel Function Regress，KFR）和人工神经网络是两种常用的非参数响应曲面法方法。

核函数回归中最著名的是Nadaraya-Watson估计方法[161]：令x=[x₁，x₂，…，x_m]^T，对于由实验得到的关于因子与响应的一组样本

S={（x₁，y₁），（x₂，y₂），…，（x_l，y_l）} （4-9）

认为过程响应y与因子x间存在一个近似的函数关系y=g（x），或者说对于上述样本有

y_i=g（x_i）+ε_i， i=1，2，…，l （4-10）

并假定ε_i独立同分布，且E（ε_i）=0，D（ε_i）=σ²<∞。选定关于原点对称的概率密度函数K（μ）为核函数，满足

∫K（μ）dμ=1 （4-11）

给定窗宽参数h>0，定义核权函数

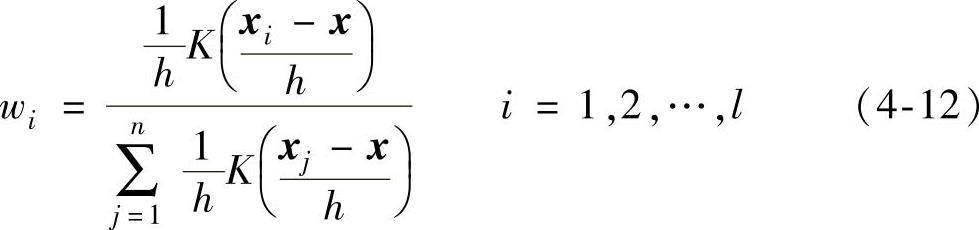
则g（x）的Nadaraya-Watson核估计定义为

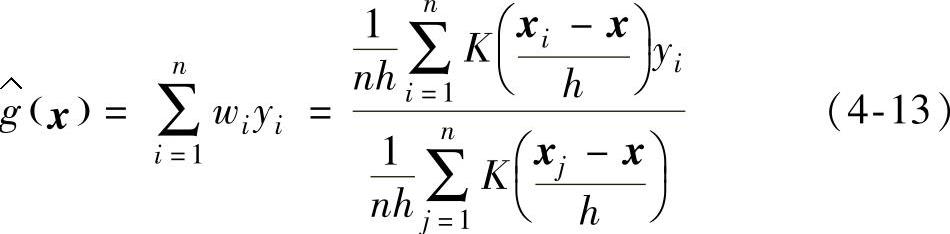
常用的核函数有均匀核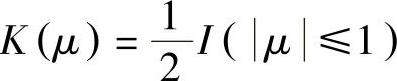、高斯径向基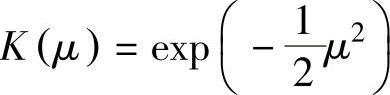核、抛物线核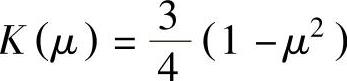等。对于Nadaraya-Watson核估计，可以证明，只要h→0，nh→∞，则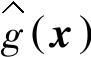是g（x）的一致估计量。也就是说，当nh→∞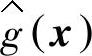，将依概率收敛于g（x）。并且理论上存在一个最优的窗宽参数h，使得预测的均方误差

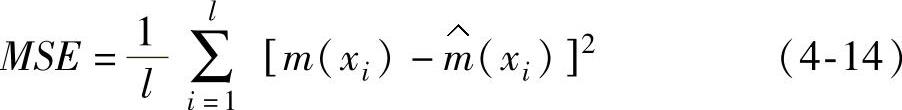
最小。但实际上这一最优值并不易得到，目前一般采用交叉验证法（cross-validation）和惩罚函数法（penalizing function）等来寻找次优的h值。

人工神经网络是基于人工智能理论中的联结理论构建的智能仿真模型，模仿生物神经系统，通过相互联结的网络结构和一定的学习机制去模拟过程输入与输出之间的关系。理论上一个三层BP人工神经网络可以逼近任意复杂的非线性关系，如果用三层BP人工神经网络去拟合式（4-10）中的g（x），则成为基于人工神经网络的响应曲面法。