基于Hopfield神经网络的突变自相关过程监控方法

1.基本原理

考虑式（3-7）所描述的平稳自相关过程，由于E（x_t）=s，因此可以将t时刻的s值看做该时刻的原形；另外，对式（3-5）展开有

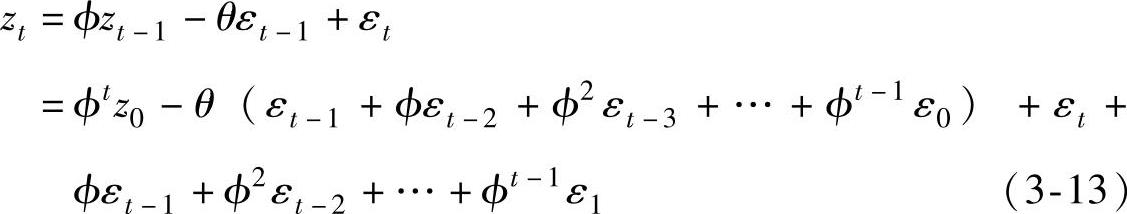
在t=0时，若令z₀=0，ε₀=0，则有

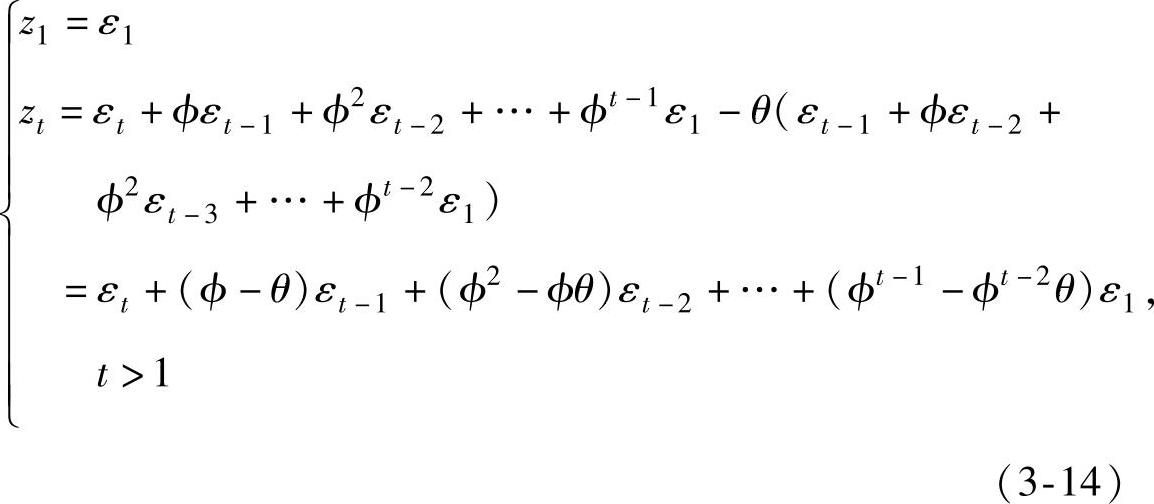
上式说明，z_t是由白噪声序列ε₁，ε₂，…，ε_t的线性组合而成的。因此可以将z_t看做t时刻的噪声项，而x_t则成为t时刻原形s被z_t污染后的样本。

2.算法步骤

对于式（3-7）所示均值阶跃型突变过程，由于s=0代表过程正常，s≠0代表过程失控，于是通过对s进行适当的编码，可以将过程正常或过程失控两种状态分别作为两个吸引子存储到Hopfield人工神经网络中。而对于待检测的x_t，将其编码后作为网络输入，通过联想功能滤去z_t的影响，使其收敛到稳定态，再根据稳定态的类型判断过程是否正常。

具体步骤如下：

步骤1：吸引子编码。

设在第k₀（k₀≥2）时刻，过程均值出现了大小为s₀（s₀>0）的阶跃型突变，于是当t≥k₀时有E（x_t）=s₀，而当t<k₀时有E（x_t）=0。以k₀时刻作为基准点，等距离地向前、后各延伸l个时刻。共计2l个时刻。对这2l时刻内的s值进行编码，若过程均值未发生突变（s=0），则将s值编码为-1，若过程均值发生突变（s>0），则将s值编码为1，由此形成表3-1所示的吸引子编码。

表3-1 过程正常与异常时的吸引子编码

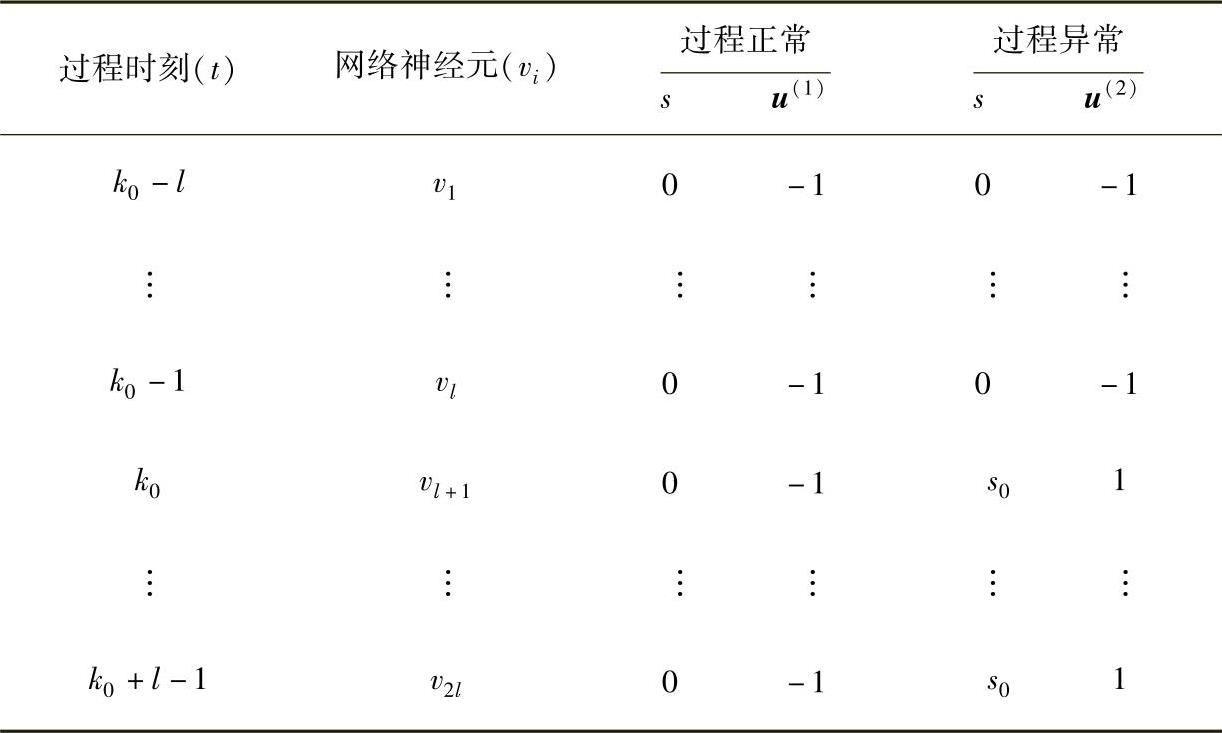
采用上述编码方案，吸引子u^（1）表示在这2l个时刻内s值未发生变化，即过程正常；吸引子u^（2）表示s在第k₀时刻出现了阶跃型突变，即过程发生异常。

步骤2：模式记忆与权值设计。

由式（2-22）及u^（1）、u^（2），可计算出网络的权值。

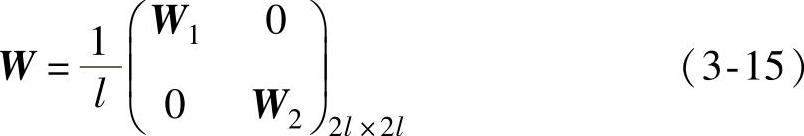(https://www.xing528.com)

其中

由于u^（1）（u^（2））^T=0，说明u^（1）与u^（2）正交。因此根据外积法的性质，可将过程正常和过程异常的模式作为吸引子存储到了Hopfield人工神经网络之中，该网络共有n=2l个神经元。

步骤3：待检测样本编码及输入向量生成。

t=k₀-l，k₀-l+1，…，k₀-1，k₀，k₀+1，…，k₀+l-1时刻的x_t值编码规则如下

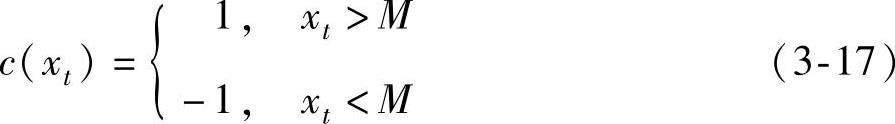
其中

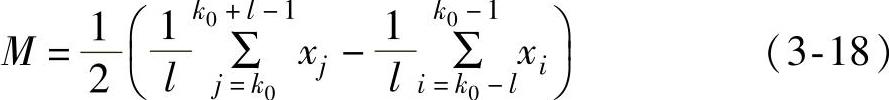
M的含义是均值突变前l个时刻过程质量特性的均值与突变后l个时刻过程质量特性的均值之差的1/2，以M作为判断阈值，当某时刻的质量特性值大于M时，将其编码为1，当值小于M时则编码为-1。这样，可以根据某一时刻前后过程均值的变化来检测过程是否发生了阶跃型突变。

进一步地，网络的输入向量为

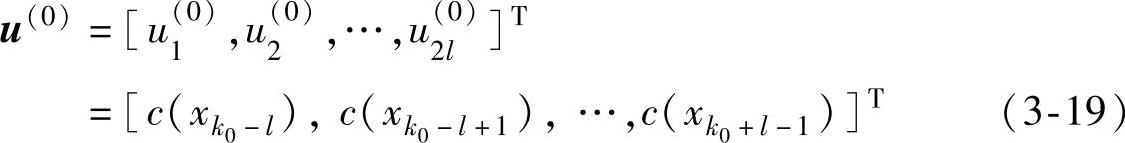
步骤4：联想与模式判别。

利用式（2-24）对u^（0）进行迭代运算至网络达到稳定态，与u^（1）、u^（2）相比，确定过程是否正常。根据Hopfield人工神经网络的性质，除了设定的吸引子之外，网络中将伴随产生其他多余的稳定状态（伪吸引子）。如果第4步网络稳定后的吸引子类型与u^（1）、u^（2）均不相同，则说明网络稳定到了伪吸引子。此时需要增大l的值，重复步骤1～4，直至网络稳定至u^（1）或u^（2）为止，由此判断过程正常或异常，此时的l值即为网络自k₀时刻起检测到过程异常所需的样本量，也即平均链长ARL。

3.算法流程图

根据均值阶跃型突变自相关过程质量监控算法步骤，得到该算法流程图如图3-4所示。