过程均值的阶跃型突变与渐进型漂移分析

1.均值阶跃型突变

根据生产实际，自相关过程质量特性的异常状态主要有两种：均值的阶跃型突变和均值的渐进型漂移。均值的阶跃型突变是指自某一时刻起，过程均值突然发生大小为s的增大或减小，而且自该时刻起，一直保持在新的水平不变。该异常状态的统计学描述如下：

令x_t代表过程的质量特性的时间序列观测值，其中t=1，2，…，k代表时间观测点，且有

x_t=z_t+s （3-7）

式中 z_t——式（3-6）中的平稳自相关过程；

s——由异常原因引起的过程质量特性均值的突变。

当z_t为平稳ARMA（1，1）序列时，根据式（3-6）和式（3-7），x_t将变为均值为s，方差为1的序列，其方差也不随t的变化而发生变化。图3-2所示为在第t=50时刻之后，过程均值出现了大小为s的阶跃型突变。

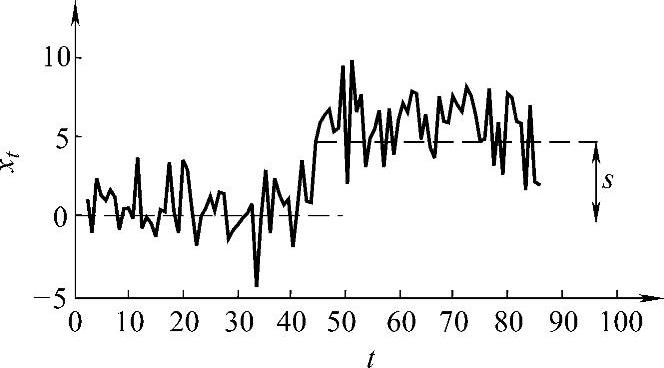
图3-2 自相关过程均值阶跃型突变示意图(www.xing528.com)

2.均值渐进型漂移

均值的渐进型漂移是指自某一时刻起，过程均值以一个不变的比例因子发生连续变化，其变化依时间推移而积累。该异常状态的统计学描述如下

x_t=z_t+r（t-k₀）

式中 r——均值渐进型漂移系数，表示从第t=k₀+1起，过程均值出现了大小为r（t-k₀）的渐进型漂移，并依时间累积。r以z_t的标准差σ为度量单位，即r=Δσ。

与均值的阶跃型突变不同的是，均值渐进型漂移情况下x_t的方差不随t的变化而发生变化，但其均值会发生连续变化。图3-3所示的平稳自相关过程，在k₀=50时刻之后，过程均值出现了r=0.1σ的渐进型漂移。

图3-3 平稳自相关过程均值渐进型漂移示意图