选择支持向量机参数的方法

支持向量机（包括支持向量分类机和支持向量回归机）由于具有良好的泛化能力而得到广泛的应用，但在应用中，使用者往往会面临参数的选择问题，这其中包括核函数的选择，以及ε-不敏感参数和惩罚参数C的选择。Cristianini和Shawe-Tay-lor^[85]，Cherkassky和Ma^[86]等学者指出，支持向量机算法的性能受所选参数的影响，不同的参数组合对应不同的分类或回归模型，而且参数的选择应该和数据集有关。Vapnik^[78]，Chapelle和Vapnik等^[87]，Soares和Brazdil等^[88]，Scholkopf和Sung等^[89]，Cherkassky和Ma^[90]，Kwok^[91]，Smola和Scholkopf^[92]，Chang和Lin^[93]等学者对此做了大量研究，但目前仍然没有一种最好的选择方法，具体应用时要根据实际问题背景进行选择。

目前支持向量机核函数和参数的选择方法大致可以分为三种：

第一种方法是根据经验风险去估计不同参数组合下的支持向量机泛化性能，然后再选择使泛化误差最小的参数组合（Muller和Ratsch等^[94]），这其中又包括交叉验证法（Cross-Valida-tion），Bayesian证据方法（Kwok^[95]），核主成分分析法等。交叉验证法是最常用的方法，但它计算烦琐，同时还需要牺牲一部分样本作为测试样本。

第二种方法是理论分析法。即通过理论分析而非经验风险去估计泛化误差的界。该界一般通过VC维来表示，但实际中函数的VC维通常难以估计，尤其是对于Gauss核，它的VC维是无穷大的，因此无法采用这种方法估计泛化误差的界。Cristianini和Shawe-Taylor^[85]研究了支持向量回归机泛化性的界，给出了不依赖于VC的泛化误差界的估计，但计算方法复杂，且存在影响估计的未知参数。

第三种方法是采用启发式算法来进行参数选择。如Smola和Scholkopf^[96]，Soares和Brazdil等^[88]，但这种方法需要借助于专家经验，或者需要较大的样本量，用以数据从中学习并设定支持向量机参数。

有关核函数、ε参数、C参数选择的主要研究内容可以概括如下：

1.核函数的选择

支持向量回归机引入核函数是为了避免非线性变换后产生的高维特征空间计算的“维数灾难”，不同的核函数对应着不同的非线性变化，因此选择合适的核函数对于提高支持向量机的泛化性能具有重要意义。核函数以满足Mercer条件为基础，但Cha-pelle和Vapnik^[97]指出，在实际应用中，核函数的选择还应该和过程的先验知识以及样本数据的分布特性有关。核函数的选择又包括核函数类型与核参数的选择。除了本节介绍的常用的核函数（如多项式核函数、Gauss径向基核函数、Sigmoid核函数）之外，还有B-样条核函数、Fourier核函数等。此外，研究者还常常根据具体问题构造相应的核，例如Amari和Wu^[98]基于核函数的黎曼几何结构，通过对简单核函数的保角映射，提高了支持向量分类机中最优分类面的分辨力。

近年来，Scholkopf和Sung等^[89]，Keerthi和Lin^[99]，Cherkassky和Ma^[90]，Soares和Brazdil等^[88]，Cristianini和Campbell等^[100]众多学者通过大量的理论和对比研究证明，基于Gauss径向基核函数的支持向量回归机具有良好的拟合与泛化性能；Cristianini和Shawe-Taylor^[85]指出，通过选取适当的核参数σ，Gauss径向基核函数可以表示任意的函数。Smola和Scholko-pf^[96]指出，如果只假定数据集光滑，那么Gauss核函数是一个较好的选择；同时由于Gauss径向基核函数的参数只有一个（多项式核、Sigmoid核函数均有两个参数），有利于选择和优化，因此在支持向量回归机中得到了广泛的应用。

Shawe-Taylor和Bartlett等^[101]，Vapnik^[78]指出，根据VC维理论，基于Gauss核的支持向量机的泛化误差R（α）与样本集大小、最优分类面间隔γ以及包含所有样本集数据的最小超球体的半径R之间存在如下关系

Cristianini和Campbell等^[100]证明了对于基于Gauss核的支持向量机，其泛化误差R（α）的上界是核参数σ的光滑函数，并且他们在支持向量机的参数C固定的情形下，进一步将式（2-46）简化为

以此作为泛化误差的理论估计，用于选择最优的核参数σ。但R和γ的计算较为复杂。

2.ε-不敏感参数与惩罚参数C的选择

参数ε控制着图2-8中ε-不敏感带的宽度，同时还影响着式（2-45）中支持向量的数量，ε越大，支持向量的数目越少，模型也就越平坦（复杂性降低）；ε越小，支持向量的数目就越多，模型的复杂性就越高，也就越容易出现“过学习”现象。考察式（2-39）可以发现，C作为对超出ε-不敏感区的样本的惩罚因子，它实际上还起着一种在模型平坦性与经验误差之间的折中作用。如果C选取得比较大，即对超出ε-不敏感区的样本实施较严厉的惩罚，或者说追求一个很小的经验风险，那么将导致一个相对大的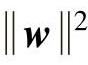，于是模型的复杂性将会增大。反之，若选取较小的C，则允许相对较大的经验风险，而模型的复杂度将降低。可见ε与C共同决定着模型的泛化性能。(www.xing528.com)

Vapink^[78]等提出采用先验知识及专家经验来确定这两个参数；Scholkopf和Smola等^[102]提出ν-支持向量回归机，以此为一个参数ν代替ε，并且有0≤ν≤1，ν的选择范围比ε小，因此更容易被确定；Chalimourda和Scholkopf^[103]对ν的选择作了进一步的讨论。但实际上，ν的选择也比较困难。Mattera和Haykin^[104]提出根据支持向量回归机拟合模型中支持向量占样本的比率SV%来确定ε，这一比率应控制在50%左右，但实际应用中并非如此；同时他们还提出参数C应该与样本输出的极差相等，但这种方法没有考虑离群值对极差的影响。Kwok^[91]指出，ε与过程误差（服从正态分布）的方差之间存在一定的线性关系；Keerthi与Lin等^[99]研究了基于Gauss核函数的支持向量分类机的参数C与核参数σ的渐进性能；Smola和Murata^[105]提出ε的渐进性选择方法，并且建议ε应该与误差方差的大小成比例，但这种方法没有考虑样本含量的影响；Cherkassky和Ma^[86，106]提出一种实用性的支持向量机参数ε与C的选择方法。该方法不需要测试样本集，通过对样本含量，样本数据及其误差的分析直接确定ε与C，具体可描述如下：

对于式（2-25）所示的样本集S={（x₁，y₁），（x₂，y₂），…，（x_l，yl）}，设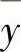代表y_i的平均值，σ_y代表y_i（i=1，2，…，l）的标准差，则参数C选择为

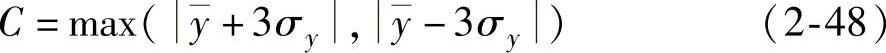
与Mattera和Haykin^[104]提出的方法（即C与y_i的极差相等）相比，该方法既考虑了样本的分布，同时又避免了离群值的影响。

Kwok^[91]、Smola和Murata^[105]等众多的研究者指出，ε应与输入噪声的水平成正比。Cherkassky和Ma同时还指出，ε还应该和样本量的大小相关，样本量越大，ε应越小。设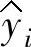代表y_i的拟合值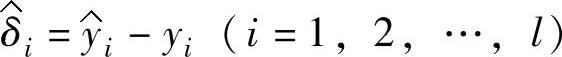，，表示输出的拟合误差。并且假定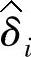独立同分布，且均值为0，方差为σ²_P。令

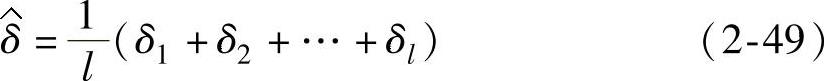
根据中心极限定理可知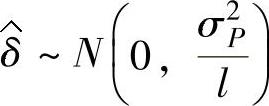，。Cherkassky和Ma认为，ε的选择应该和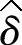的方差相关，综合考虑样本量l的影响，存在如下影响关系

由此，Cherkassky和Ma给出了确定ε的经验公式

对于过程噪声的方差σ²_P，现有研究一般是直接从样本集数据中估计，Cherkassky和Shao等^[107]提出

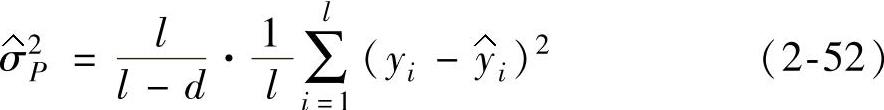
式中 d——估计量的自由度，对于线性回归来说，d就是自由变量的个数；但对于其他形式的回归，例如支持向

量机回归，d值并不容易计算。

通过对不同形式和维度、不同误差分布形式的样本集的回归，Cherkassky和Ma指出，在核函数固定的情形下，由式（2-51）与式（2-48）确定的ε与C值接近于最优值，而且可以取得较小的泛化误差，说明了该方法的优越性。