首先考虑线性回归问题,即限定所寻求函数f(x,α)为线性函数
f(x,w)=(w·x)+b (2-30)
假设所有样本数据可以在ε-不敏感函数的意义下无误差地用式(2-30)拟合,其参数w的求取可以表示如下
在约束不能满足的条件下,引入松弛变量ζ(∗)=(ζ1,ζ1∗,ζ2,ζ2∗,…,ζl,ζl∗)和惩罚参数C得到如下的最优化问题
对于非线性的回归问题,引入非线性变换φ(xi)将原始样本集映射到高维的Hilbert空间中,在此空间中原问题可用线性回归方法解决。具体来说,引入从输入空间Rn到Hilbert空间H的变换
x∈Rn→H
φ: (2-33)
x|→φ(x)
把样本集式(2-25)映射为
S′={(φ(x1),y1),(φ(x2),y2),…,(φ(xl),yl)} (2-34)
可以证明,优化算法式(2-32)在映射后的特征空间只涉及φ(xi)与φ(xj)的内积运算而不涉及单独运算,如果能定义某类函数K(xi,xj)=φ(xi)·φ(xj),则甚至不必知道φ(xi)与φ(xj)的具体形式。这样就可以极大地简化映射后的高维空间中的向量运算。统计学习理论指出,根据Hilbert-Schmidt原理,只要一种运算满足Mercer条件,它就可以作为内积使用。
Mercer条件表述为:对于任意的对称函数K(x,x′),它是某个特征空间中的内积运算的充分必要条件是,对于任意的φ(x)≢0且∫φ2(x)dx<∞,有
∬K(x,x′)φ(x)φ(x′)dxdx′>0 (2-35)
函数K(x,x′)又称为核函数。常用的核函数有
1.多项式核函数
K(x,x′)=(x·x′+c)d (2-36)
式中 c≥0;
d——任意正整数。(https://www.xing528.com)
2.Gauss径向基核函数
3.Sigmoid核函数
K(x,x′)=tanh(K(x,x′)+v) (2-38)
式中,K>0,v<0。
此时最优化问题变为
通过求解其对偶问题,可以如下支持向量回归机算法:
1)设已知的样本集
S={(x1,y1),(x2,y2),…,(xl,yl)} (2-40)
式中 xi∈χ=Rn,yi∈R(i=1,2,…,l)。
2)选取适当的核函数K(x,x′)和正数ε和C,构造并求解最优化问题
利用Lagrange函数及Kuhn-Tucker条件,求得最优解为
3)构造决策函数。
式中 b——按式(2-44)计算。
选择位于开区间(0,C)中的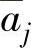 或
或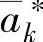 。若选到的是
。若选到的是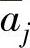 ,则
,则
若选到的是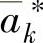 ,则
,则
对于式(2-45),同支持向量分类机一样,当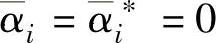 ,样本xi对回归方程是没有贡献的,而
,样本xi对回归方程是没有贡献的,而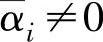 或
或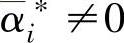 对应的xi将参与到回归方程的构建中,因此将这些xi称为支持向量。由于除了核函数外,参数ε需要人为指定,因此该算法又称为ε-支持向量回归机(ε-SVR)。
对应的xi将参与到回归方程的构建中,因此将这些xi称为支持向量。由于除了核函数外,参数ε需要人为指定,因此该算法又称为ε-支持向量回归机(ε-SVR)。
在支持向量回归机中,如果计算出的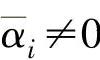 或
或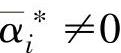 ,则称样本集式(2-40)中对应的xi为支持向量。支持向量具有稀疏性,也就是说,并不是所有的样本点都是支持向量。
,则称样本集式(2-40)中对应的xi为支持向量。支持向量具有稀疏性,也就是说,并不是所有的样本点都是支持向量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




