【摘要】：回归估计问题可以描述如下：设给定训练集S={，，…，l） 假定训练集是按照χ×Υ上的某个概率密度F（x，y）选取的独立同分布的样本点，又设给定损失函数L，分布回归估计就是利用S中的数据，在函数集{f（x，α）}中寻找一个最优的函数{f}，使预测的期望风险R（α）=∫LdF（x，y） 最小。可见为使泛化误差最小，应同时最小化拟合误差与置信范围，这就是结构风险最小化原则的基本思想。
回归估计问题可以描述如下：设给定训练集
S={（x1，y1），（x2，y2），…，（xl，yl）}
xi∈χ=Rn，yi∈Υ=R（i=1，2，…，l） （2-25）
假定训练集是按照χ×Υ上的某个概率密度F（x，y）选取的独立同分布的样本点，又设给定损失函数L（y，f（x，α）），分布回归估计就是利用S中的数据，在函数集{f（x，α）}中寻找一个最优的函数{f（x，α0）}，使预测的期望风险（或泛化误差）
R（α）=∫L（y，f（x，α））dF（x，y） （2-26）
最小。这里概率密度F（x，y）未知，{f（x，α）}由某些算法LM来实现，其中α∈Λ，表示广义的参数。LM的输出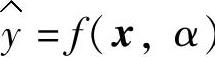
作为y的估计。称L（y，f（x，α））为损失函数，是由于用{f（x，α）}估计y造成的损失。模型的经验风险（即拟合误差）Remp（α）与R（α）之间有如下的关系(www.xing528.com)
R（α）≤Remp（α）+Φ（h，n） （2-27）
式中 h——{f（x，α）}的VC维，反映其学习能力的指标；
Φ（h，n）——置信范围。
可见为使泛化误差最小，应同时最小化拟合误差与置信范围，这就是结构风险最小化原则的基本思想。传统的最小二乘法、核函数法、人工神经网络等只注重最小化拟合误差，因而得不到最小的泛化误差。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
