人工神经网络模型与算法探析

1.基本的神经元

神经元是对生物神经元的一种模拟与简化，是人工神经网络的基本处理单元。1943年McCulloch和Pitts定义了简单的人工神经元模型，被称为M-P模型。该模型可以用图2-2来描述。神经元的输入向量为x=[x₁，x₂，x₃，…，x_n]^T，来自于外部环境或网络内其他第i个神经元输出。

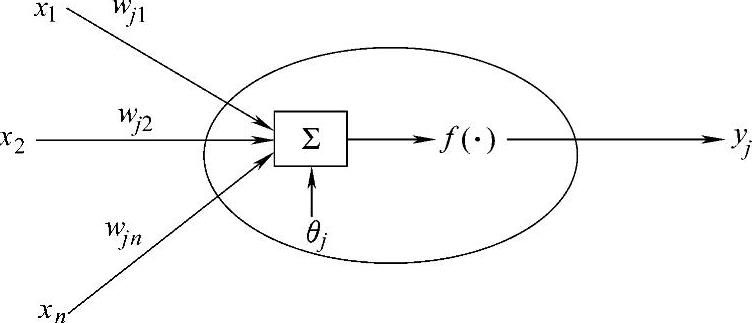
图2-2 人工神经元模型

在该神经元模型中，向量w_j=[w_j1，w_j2，w_j3，…，w_jn]^T称为权值向量，代表两个神经元之间的联接强度，其中w_ij代表处理单元i和j之间的联接权值，通过对不同神经元之间联接权值的调整和训练可以得到不同的输出。θ_j称为偏置，y_j是该神经网络的输出，有

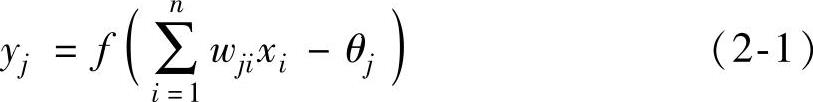
或

y_j=f（w_j^Tx-θ_j） （2-2）

式（2-1）中的f被称为激励函数，决定神经元的输出，一般具有非线性特征，常用的激励函数有：

（1）阈值型函数

1）阶跃函数

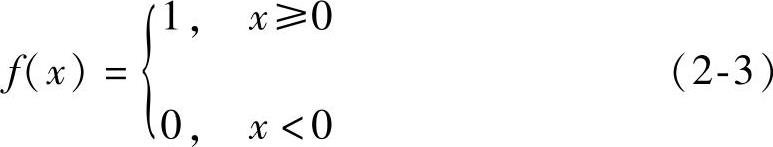
2）符号函数

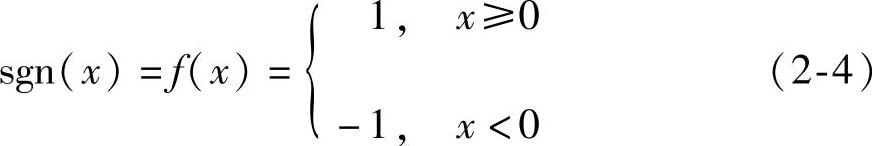
（2）连续型函数

1）饱和型函数

2）双曲正切函数

f（x）=tanh（x） （2-6）

3）Sigmoid函数。神经元的状态与输入作用之间的关系是在（0，1）内连续取值的单调可微函数，称为Sigmoid函数，简称S型函数。

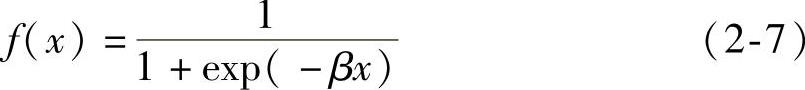
式中 β——斜率系数，β>0。

4）高斯型函数

5）组合连续型函数。即上述连续型函数的分段组合，但需保证连接处函数的连续性。

2.感知机模型

感知机模型是一种提出较早的、较为简单的人工神经网络形式，可用于对线性可分样本的分类。它由输入层和输出层两层构成，输出层仅有一个神经元的感知机结构，如图2-3所示。

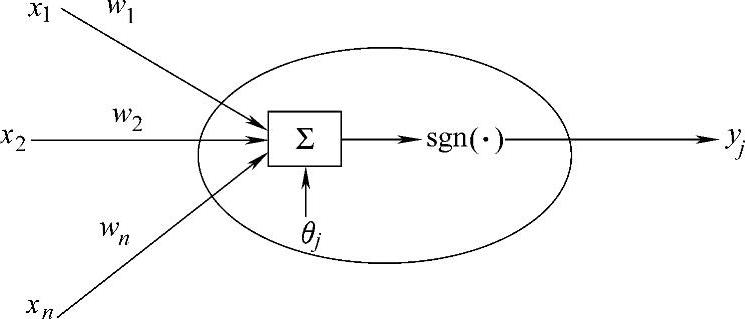
图2-3 单神经元感知机模型

外界信号经过加权输入最后一个单元，该单元采用式（2-4）所示的符号函数作为激励函数，其输出为1或-1。设网络的输入向量为：x=[x₁，x₂，x₃，…，x_n]^T，对应的期望输出为d；由输入自输出的权值向量为w=[w₁，w₂，w₃，…，w_n]^T，则网络按下列规则进行学习，即按照某种规则对权值进行调整，使得感知机的输出和期望输出一致。

感知机学习算法步骤如下：

步骤1 初始化。将权值向量和阈值赋予随机数，令t=0。

步骤2 连接权值的修正。对于每个样本的输入x₁，x₂，…，x_n与输出y完成如下计算：

1）计算网络输出

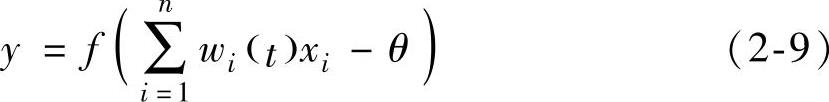
其中

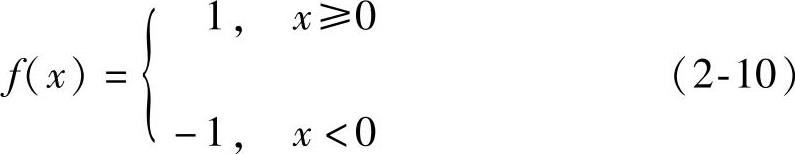
2）计算输出层单元期望输出与实际输出的误差

e=d-y （2-11）

3）若e=0，则说明当前样本输出正确，不必更新权值，否则更新权值和阈值

式中 α——学习率，用于提高学习过程的收敛性。

步骤3 对所有的输入模式重复步骤2，直到所有的样本输出正确为止。

可以证明，神经元的感知机学习算法对于线性可分的样本是收敛的，但无法实现异或形式的分类问题。

3.前向人工神经网络模型

前向人工神经网络又称为前馈型人工神经网络，该网络由多层多个神经元组成。神经元按输入输出顺序分层排列，分为输入层、隐层和输出层，每一层的神经元只接受前一层神经元的输入，如图2-4所示。图中x=[x₁，x₂，x₃，…，x_n]^T为输入向量，W¹，W²，…，W^k为各隐层的权值矩阵，y=[y₁，y₂，y₃，…，y_n]^T为输出向量。

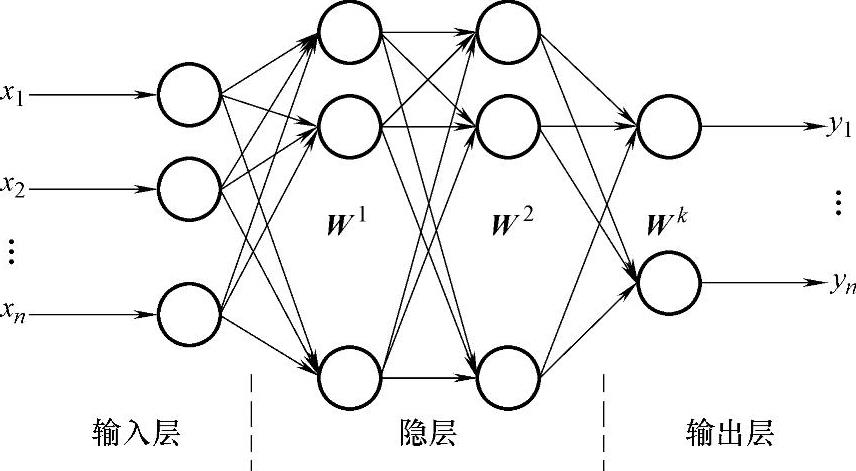
图2-4 前向人工神经网络模型(www.xing528.com)

理论上，一个三层的前向人工神经网络能够逼近任意复杂的连续非线性函数，在函数拟合、回归预测等领域有着广泛应用。对于多层前向人工神经网络，需要解决的关键问题是权值调整的学习算法，这其中最著名的是Rumelhart和McClelland提出的BP算法，而采用BP算法调整网络权值的前向神经网络也被称为BP网络。

多层前向人工神经网络的节点（即神经元）如图2-5所示，该节点的输入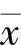定义为输入信号加一个偏置项的加权和（使用指数函数作为激励函数的示例）

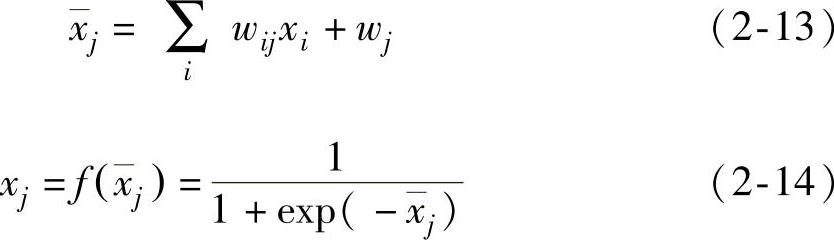
式中 x_i——位于前一层的任一节点i的输出；

w_ij——连接节点i和j的权值；

w_j——节点j的偏置，节点权值的改变将改变节点的行为，

继而改变整个网络的行为。

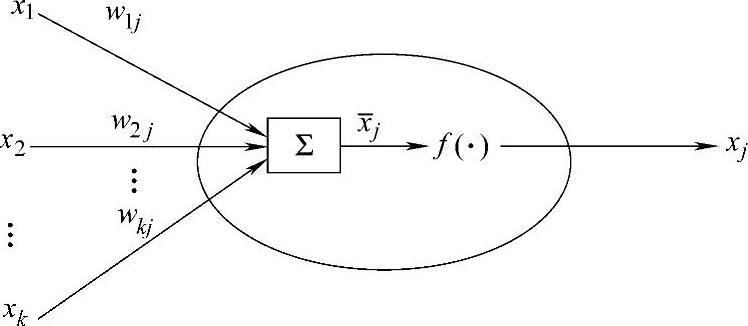
图2-5 多层前向人工神经网络的节点

定义第p个输入—输出对的平方误差指标为

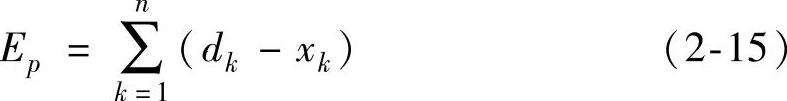
式中 d_k——节点k的期望输出；

x_k——第p个数据对输入部分出现时节点k的实际输出。

为了求得梯度向量，节点i的误差项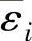定义为

由链式法则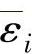，的递归公式可写作

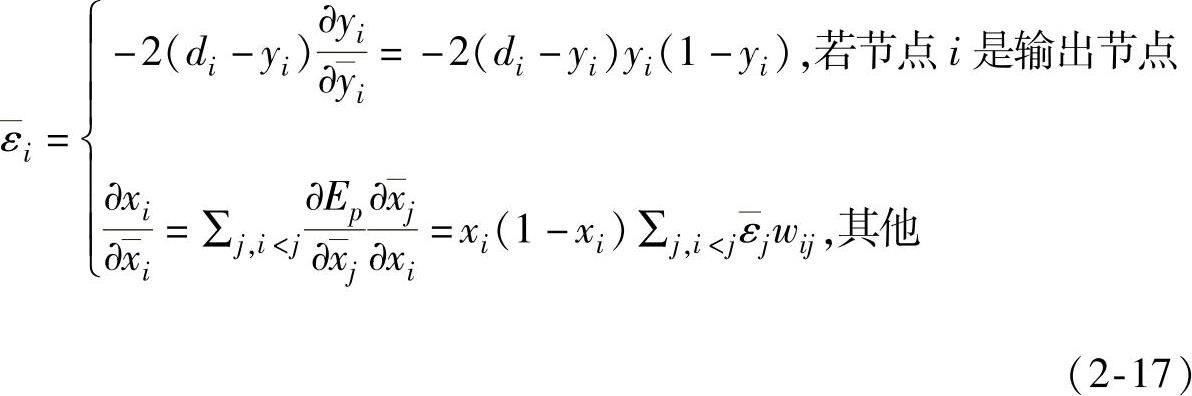
式中 w_ij——从节点i到节点j的连接权值，若没有直接联接，w_ij取作零。

对于在线的学习方式，每输入一个样本，权值就更新一次，权值更新w_ki等于

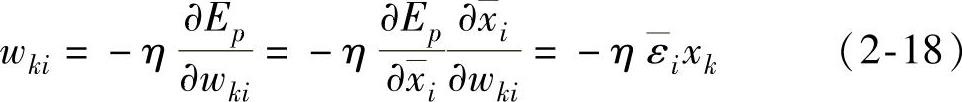
式中 η——反映收敛速度和学习中权值稳定性的学习速率。每个节点偏置项的更新公式可以类似推出。

对于离线的学习方式，只有在给出整个样本集或经过一个周期后才更新连接权值wki

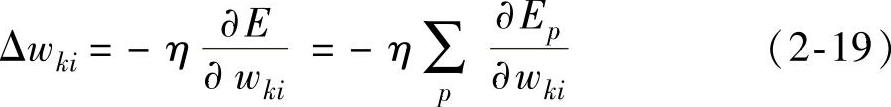
写成向量形式为

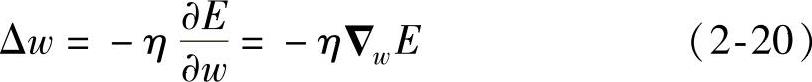
式中 E=∑_pE_p。

本算法的具体步骤如下：

步骤1 用小的随机数初始化权值W。

步骤2 输入一个样本，用现有的权值W网络计算各神经元的实际输出。

步骤3 根据式（2-15）计算目标值与实际输出的偏差E_p。

步骤4 根据式（2-18）、式（2-19）调整权值。

步骤5 返回步骤2重复计算，直到误差。

BP算法的一个明显缺点就是学习速度较慢和易陷入局部极小点而无法到达全局最小点，这在一定程度上限制了它的应用。针对这一问题，研究者进行了广泛的探索，提出了不少改进的BP算法，例如使用动量因子、自适应学习速率、归一化权值调整、多个BP人工神经网络集成使用等。

4.离散型Hopfield人工神经网络模型

与基于权值训练的感知机、前馈型人工神经网络不同，Hopfield人工神经网络属于反馈型网络，是一种模拟生物记忆功能的联想学习网络。它拥有良好的容错和纠错性能，其任一神经元的输出经其他神经元后又反馈给自身，由各神经元的权重和连接结构来实现记忆与联想的功能，可以把被污染的、畸变的输入样本恢复成完整的原形，被广泛应用于分类、识别、优化计算等领域^[76]。Hopfield人工神经网络分为连续型和离散型两种，图2-6所示为离散型Hopfield人工神经网络^[77]示意图。

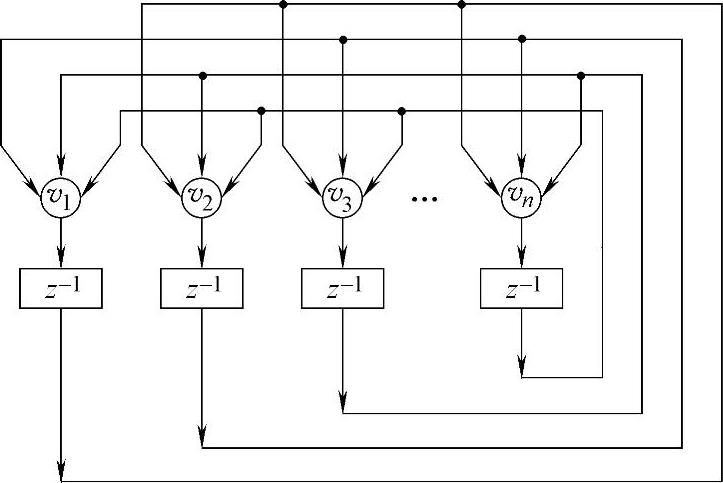
图2-6 离散型Hopfield人工神经网络示意图

离散型Hopfield人工神经网络的工作过程可以分为记忆阶段和联想阶段。设网络共有n个神经元，对各神经元赋值为-1或+1，则网络最多可以有2ⁿ个不同状态，并且构成一个离散的状态空间。首先将m个模式x_p（p=1，2，…，m，m＜n）编码作为吸引子存储于网络之中；而后将x_p被噪声e_i污染后的新值y_i=x_i+e_i的编码作为网络输入，通过网络的动力学迭代运算，滤去噪声的影响，使其最终收敛至x_p，从而达到联想和还原的目的。

记忆阶段吸引子的存储是通过合理设置Hopfield人工神经网络神经元之间的连接权值来实现的：对需要存储的m个样本x_p以某种方式进行编码，形成相应的记忆模式u^（p）（p=1，2，…，m）u^（p）=[u₁^（p），u₂^（p），…，u_n^（p）]^T，u_i^（p）∈{_-1，1}，i=1，2，…，n （2-21）

然后计算网络任意两个神经元之间的连接权值W=（w_ij）n×n，其中

经过式（2-22）计算得到的权值，可以将u^（p）所代表的m个模式，作为m个吸引子存储到网络的状态空间中。

在联想阶段，设v（s）=[v₁（s），v₂（s），…，v_n（s）]^T代表s=0，1，2，3，…时刻的网络神经元状态，首先将需要识别的某一新值y_i以特定方式进行编码，作为网络神经元的初始状态v（0）

v（0）=[v₁（0），v₂（0），…，v_n（0）]^T （2-23）

然后根据公式

v（s+1）=sgn（Wv（s）），s=1，2，3，… （2-24）

计算各时刻的网络神经元状态。若在s+1时刻对所有神经元v_i（i=1，2，…，n）同时进行更新，则称为同步更新方式；若在s+1时刻对所有神经元v_i（i=1，2，…，n）逐个进行更新，则称为串行更新方式。可以证明，至某一时刻s，采用同步更新方式的离散型Hopfield人工神经网络最终表现为两种状态：其一，所有神经元的状态不变，即v（s+1）=v（s），网络达到稳定点；其二，v（s）≠v（s+1）=v（s-1），网络稳定于周期为2的振荡环，稳定后各神经元的状态v（s）称为网络输出，将v（s）与记忆模式u^（p）相比较，即可得出网络对于输入y_i的联想结果。