1. 现金流量及现金流量图
资金等值计算常用现金流量的概念和现金流量图的图解方式进行,在此基础上,把不同时期的价值换算成相同时期的价值,然后进行对比。
现金流量包括现金流入与现金流出。现金流入是指在一定周期内的实际现金收入,现金流出是指在一定周期内的现金支出。一般把现金流入作为正值,现金流出作为负值。把现金流入与现金流出的代数和称为净现金流量。
所谓现金流量图是一个工程项目在一定周期内资金流动状况的图解方法。现金流量图的基本要素为:
(1)现金流量图时间坐标,如图1.5.2所示。
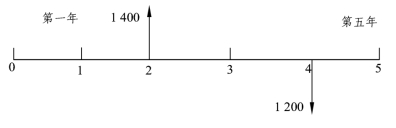
图1.5.2 现金流量图
如图所示,水平线就是时间标度,自左向右,每一格表示一个时间单位(年、月、日),本例以年为单位,时间标度表示年末,如“1”表示第一年年底,同时表示第二年年初。
(2)正现金流量与负现金流量,用箭头表示。向上箭头表示现金流入,即正现金流量,可标上数量,如第二年年末有一笔收入,见图1.5.2的1 400元。向下箭头表示现金流出,即负现金流量,可标上数量,如第四年年末有一笔付款,见图1.5.2的1 200元。
(3)现金流量图与所表示的立脚点有关,如图1.5.3所示。
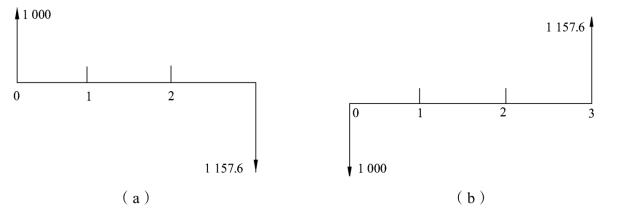
图1.5.3 两种立脚点的现金流量图
图1.5.3(a)是对借款人说的,第一年初借款1 000元,是一笔收入,3年后还款1 157.6元,是一笔支出。图1.5.3(b)是对贷款人说的,第一年初贷出款项 1 000元,是一笔支出,3年后可收回1 157.6元,即为一笔收入。
2. 等值资金与等值计算
资金具有时间价值的观点,既表明了一定数量的资金在不同时间会有不同的价值,同时也说明了在不同的时间,数量不等的若干资金可以具有相等的价值,例如,当前的 99 万元与1年后的100万元数量上并不相等,但在年利率为1% 的条件下,二者是等值的。
我们把特定利率下,在不同时间(时期、时点)上绝对数额不同,而价值相等的若干资金称为等值资金。影响资金等值的因素是:① 资金额的大小;② 计息周期,③ 利率的大小。
利用等值概念,可以把某一时间(时期、时点)上的资金值按一定利率换算为另一个时间上的资金值,这一换算过程叫作资金的等值计算,银行借贷利息的计算是常见的资金等值计算问题。
在各种资金等值计算中,我们特别把某一时间上的资金值,换算成与之等价的、几个周期前或后的资金值计算叫“贴现”或“折现”。把与某一时间上资金等值的几个周期前的资金值称为现值;把与现值等价的未来某时间上的资金值称为将来值或未来值。这里所说的“现值”或“未来值”是一个相对的概念。
对某个第n 周期上的资金值来说,在确定利率下,相对于n+n′周期上的资金值,它是现值;而对n-n′周期上的资金值来说,它是将来值。
3. 资金等值计算的基本方法
资金等值计算,也就是资金时间价值或货币的利息计算。
其基本的计算方法分为单利法和复利法两种:
(1)单利法。就是资金运动过程中,只是本金计息,而利息不再生息的计算方法。
① 未来值计算:
![]()
式中:P——资金的现值(元);S——n年后的未来值(本利和)(元);i——每年的单利利息率(%);n——年数(年);(1+in)——称单利计息未来值系数。
② 现值计算:
![]()
式中符号同上,(1+in)-1称单利计息现值系数。
(2)复利法。是在资金运动过程中,不仅本金计息,而且先前周期的利息在后继的周期中也要计算利息的计算方法。
① 未来值计算:如现有资金P 元,每年利息率为i,1年后的本利和为P(1+i)元,两年后的本利和为P(1+i)2……n年后的本利和为P(1+i)n,故:
![]()
上式中的(1+i)n通常称为复利计息未来值系数,式中符号同上。
② 现值计算:如已知资金的未来值S,利息率i和年数n,则求现值P的公式为:

上式中(1+i)-n通常称为复利计息现值系数。
资金有各种不同情况,使用和计息方法也各有不同,因此资金利息具体计算方法则各有所别,但都是从上述两类未来值和现值计算公式演变而来的。现举例如下:
a. 无息贷款:P=S
b. 单利计息:分年贷款,n 年来的本利和为:(https://www.xing528.com)
![]()
式中:R1,R2,…,Rn——各年贷款金额;
P =R1+R2+…+Rn。
例 某工程合计贷款1 000万元,第1年贷款 500万元,第2年贷款300万元,第3年贷款200万元,年单利率i=3%,问第3年末的本利和为多少?
解
S=1 000+500(0.03×3)+ 300(0.03×2) + 200(0.03×1) = 1 069(万元)
c. 复利计息,分期贷款,n 年末的未来值是:
![]()
例 某工程贷款1 000万元,第1年贷款400万元,第2年贷款300万元,第3年贷款300万元,复利计息,年利率为12%,问第3年末的本利和为多少?
解
![]()
d. 复利计息,分期等额发生款项本利和:

这个公式,由等比数列求和公式而来。
式中:R——分期等额发生额。
例 某工程投资预算总额12亿元,6年建成,每年贷款2亿元,i复=8%,求第6年末的本利和为多少?
解 当金额发生在年初时,等比数列首项的形式是R(1+i)

当金额发生在年末时,等比数列首项的形式是R。
例 某工程投产后预计前5年每年可盈利200万元,如年复利率为8%,问到第5年末时共盈利多少?
解
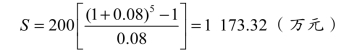
③ 等额序列现值公式。知道年复利率、年数和每年等额发生的金额时,求现值资金总额的计算方法为:

此公式实为![]() 的变形,因为复利计息,分期等额发生时,n年后的未来值为:
的变形,因为复利计息,分期等额发生时,n年后的未来值为:

例 仍用上例数据,某工程投产后,预计前5年每年盈利200万元,如复利率为8%,问前5年的利润折合为现值是多少?
解

④ 资金偿还公式。已知某工程的现值投资为P,复利计息,年利率为i,要求在n年内以等额资金分散偿还全部投资的本利和,求每年年末应偿还的资金金额是多少?可用下列公式:

例 期初投资为 1 000 万元,i=10%,分 5 年等额偿还,求每年年末应偿还的金额是多少?
解
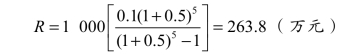
⑤ 资金偿还年限计算。当贷款总额P,每年偿还金额R,年利率i均为已知时,求资金偿还年限n可用下式:

例 已知某工程投资1 500万元,复利计息,年利率 10%,每年偿还350万元,其偿还期为多少?
解
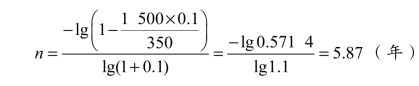
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




