如何用数学分析法预测运输需求量？

当历史统计资料准确、详细完备，事物发展变化的客观趋势比较稳定，较少有持质的突变时，一般运用数学分析法来预测运输需求量。

数学分析法主要有时间序列分析预测法、回归分析预测法（因果分析预测法）和马尔科夫预测法等。

1. 时间序列分析预测法

时间序列分析预测法的基本思想是：根据过去的历史资料，依据一组观察数值来推算事物未来的发展情况。因此，对过去的时间序列数据进行分析，就能推测事物的变化趋势，做出预测。运输需求量常用的时间序列预测方法主要有移动平均法、指数平滑法、季节系数法等。

（1）移动平均预测法。

① 一次移动平均法。移动平均预测法是按照时间的先后顺序，向前移动进行平均数计算，并以移动平均数作为下一周期的预测值。

设时间序列为：y1，y2，…，yi，…

计算公式：

式中：——第t周期的一次移动平均数；t—— 时间周期数；N——分段数据个数。

该法可以对原时间序列中的大起大落等不正常现象进行修正，剔除其中偶然因素引起的变化，从而提炼出规律性的东西。修正的程度取决于计算平均数时数据个数N的大小。N大，则修正程度就大，但时间后移也大，随之敏感性就变差；N小，则修正程度就小，但时间后移也小，随之敏感性就高。N的取值视具体情况而定。

第t+1期预测值=。

② 二次移动平均法。由于一次移动平均法往往不能发挥足够的修正作用，所以在实际应用中一般还需要进行第二次移动平均计算。

二次移动平均数计算公式：

式中：——第t 周期的二次移动平均数；——第t 周期的一次移动平均数；N——分段数据个数。

二次移动平均计算的目的不是直接用于预测，而是为了求出平均数；当移动平均数时间序列具有线性趋势时，用来修正第一次移动平均数的滞后现象。

原时间序列经过一次或几次移动平均，基本消除了偶然因素产生的影响以后，其变化趋势基本稳定，就可以根据新的时间序列建立预测数学模型。用二次移动平均法进行预测的公式为：

式中：T—— 由目前周期t 到需要预测的周期数；—— 自第t 周期起，到需要预测的以后第T周期预测数。

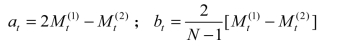
③ 用移动平均法预测铁路客运量。某铁路局集团公司 2018—2020 年各季度完成的旅客运输量如表1.3.1所示，现拟预测 2021 年各季度的旅客运输量。

第一步，计算一次移动平均数、二次移动平均数（3N=），计算结果如表 1.3.1 所示。

表1.3.1　计算结果表　单位：万人

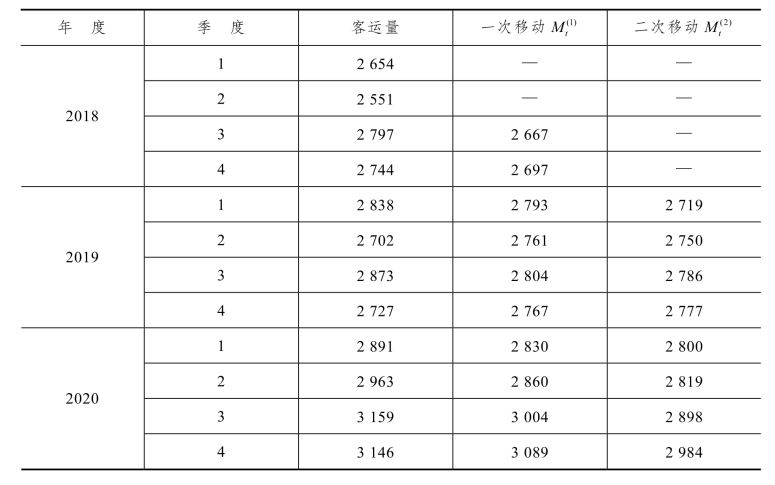
第二步，计算平滑系数at、bt，本题t取12。

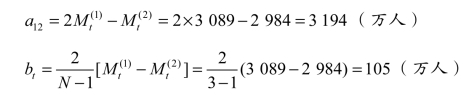
则预测公式为：

第三步，预测2021年各季度该局的客运量，则T分别取1、2、3、4代入，其预测值分别为：

第一季度：=3 194 +105 ×1=3 299（万人）

第二季度：=3 194 +105 ×2 =3 404（万人）

第三季度：=3 194 +105 ×3 =3 509（万人）

第四季度：=3 194 +105 ×4 =3 614（万人）

上述计算虽然取得了运算结果，但并不包括季节变动因子的影响，所以还要用季节变动因子进行调整。季节变动因子的测定方法是：首先计算各年的同季平均数，然后计算所有各季的季总平均数，最后，分别用各个同季平均数分别除以季总平均数，即可求得各季的季节变动因子。本例中季节变动因子的计算如表 1.3.2 所示。

表1.3.2　计算结果表　单位：万人

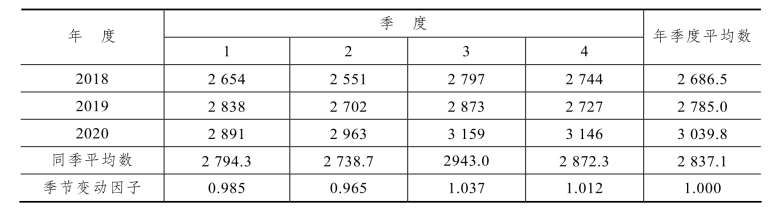
用季节变动因子对上述预测值进行调整，使之成为含有季节变动因子的预测值：

第一季度：3 299 0.985 3 250=×=（万人）

第二季度：=3 404 ×0.965 =3 285（万人）

第三季度：3 509 1.037 3 639=×=（万人）

第四季度：3 614 1.012 3 657=×=（万人）

二次移动平均法仅适用于线性趋势的数据，如果数据变化有非线性趋势，可用三次指数平滑法加以解决（见指数平滑预测法）。

（2）指数平滑预测法。指数平滑预测法是移动平均预测法的改进和发展，它既有移动平均预测法的优点，又在一定程度上克服了移动平均预测法数据存储量大的缺点。指数平滑预测法是对整个时间序列加权平均来预测的。

① 一次指数平滑法。其计算公式为：

式中：—— 第t周期的一次指数平滑平均数；yt—— 第t周期的实际数；α—— 加权系数；—— 第t－1周期的一次指数平滑平均数。

指数平滑法是将第t 周期的指数平滑数值，原封不动地作为t＋1 周期的预测值，即。

指数平滑预测法是利用平滑平均数的计算对时间序列进行修正的一种有效方法。在被预测事物中，绝大多数都存在着周期的波动和不规则变动，利用指数平滑预测法就可以在计算时对其进行修正。在修正过程中，对过去的数据分别加以不同的权数。数据越近，权数越大，数据越远，权数越小。加权系数 α 的大小，也对原时间序列的修正程度有决定性的影响。α 的大小与修正程度成反比。但是，在反应最新数据的敏感性方面，与 α 取值的大小却成正比。因此，如果指数平滑的目的在于用新的指数平滑平均数去反映时间序列中所包含的长期趋势，那么，α 取值以择小者为好。在通常情况下，取 α ＝0.1即可将季节变动的影响基本消除，将循环变动和不规则变动的影响大部分消除。 α 的取值范围：0≤ α ≤1。在长期预测中，α 一般在0.1～0.3之间。

初始值的估计。由公式（1.3.4）可知，在计算某一期指数平滑平均数时，总是需要前一期的指数平滑平均数作为起点，那么第一个指数平滑平均数怎么办？即初始值如何估计。从公式（1.3.4）可以推知项的加权系数为(1-α)t，是很小的数，即的数值对的计算结果影响很小，因此，可避免用繁锁的公式计算，采用下述两种方法估计的值：

a. 设等于原始数据的第一个数值，即y1=。

b. 设等于最初几期的原始数据的平均值，可为最初3个或最初4个或5个yi的值的平均值，即；或；或。

② 二次指数平滑法。为了提高指数平滑法对时间序列的吻合程度，可以在一次指数平滑的基础上再进行一次指数平滑，这就是二次指数平滑，其计算公式为：

式中：——第t周期的二次指数平滑平均数；α——加权系数；—— 第t－1 周期的二次指数平滑平均数。

二次指数平滑一般不直接用于预测，而是仿照二次移动平均法的原理，用来修正线性趋势变化的滞后现象。二次指数平滑后，就可以建立进行预测的公式了。其公式为：

式中：T—— 时间序列；—— 自第t周期起，到需要预测的以后第T周期预测数。

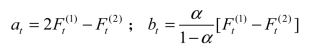
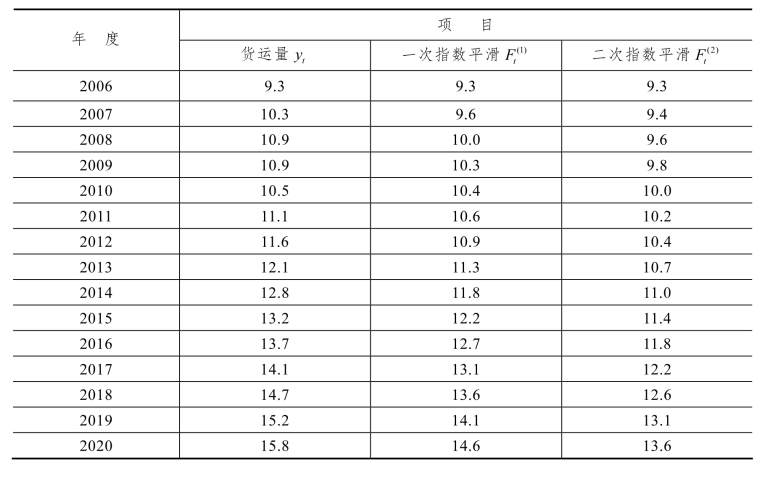
③ 用指数平滑法预测铁路货运量。某铁路局集团公司 2006—2020 年完成的货运量如表 1.3.3 所示，现拟预测该铁路局集团公司2021—2024 年货运量。

表1.3.3　货　运　量　表　单位：亿t

(www.xing528.com)

第一步，计算一次平滑平均数、二次平滑平均数（ α ＝0.3），结果见表1.3.3。

第二步，计算平滑系数at，bt。

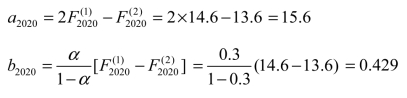
则预测货运量公式为：

第三步，进行预测

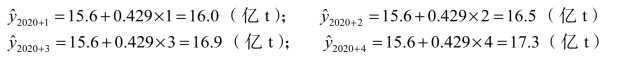
④ 三次指数平滑法。如被预测的数据曲线出现曲率时，二次指数就不适用了，此时必须采用三次指数平滑法。其计算公式为：

式中：—— 第t周期的三次指数平滑平均数；—— 第t－1周期的三次指数平滑平均数。

预测公式为：

式中：

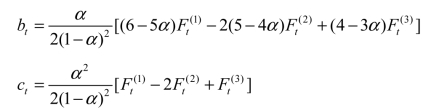
（3）预测误差的判断。时间序列往往是不规则的，在预测中会产生误差。衡量误差不能以某一次预测结果作为评定的标准，应当用统计平均的方法来判断。目前，常用的方法有平均绝对误差和平均平方差。

① 平均绝对误差。时间序列y1,y2,…,yn为观察值，,…,为预测值。

平均绝对误差为：

② 平均平方差为：

在实际应用中常采用标准差

2. 回归分析预测法

回归分析预测法，是根据事物发展的因果关系，建立数学模型，推算变量的未来值。它能够较精确地进行中、短期预测，也能适应长期预测的需要，是运输需求量预测中常用的方法。一元线性回归预测法是针对两个线性相关的变量进行预测的一种用途很广的方法。

① 一元线性回归方程的一般形式：

式中：x—— 自变量；—— 因变量；a、b—— 待定参数，又称为回归系数。

按以下公式求出参数a、b：

式中：n——数据组数。

a、b系数求出后，就可根据（1.3.12）式和x值的变化，去推算y值的未来变化。

② 相关系数r。相关系数r 是研究两个变量x、y 之间有无线性关系及其相关程度的系数。计算公式为：

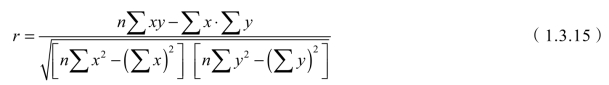
相关系数r的取值范围为：－1≤r≤1。r 的绝对值接近 1，说明x和y线性关系越好；否则线性关系越差；其值接近0，就可认为二者完全没有线性关系。

③ 置信区间的估算问题。通过回归方程（1.3.12）可由x值预测y值（），由于因变量y受自变量x 以外其他因素的影响，实际观测值与其对应预测值之间常有误差存在。如果预测值y绕拟合回归线散布较大。那么，根据回归方程计算出的预测值与实际观测值的偏差也大，反之亦然。为了判断误差大小，就必须弄清实际值的散布范围，我们需要用数理统计方法来计算置信区间。

a. 标准离差S (y)。各预测值的标准离差S (y)表示回归直线周围个体数据点的密集程度。S (y)的计算公式为：

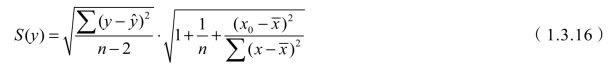
式中：n－2——统计量自由度；x0——预测点的自变量的数值。

b. 置信区间的计算公式。

上限：

下限：

式中：α——显著性水平；n－2—— 统计量自由度；(tα/2,n－2)——t分布临界值，可由t 分布表查得。

④ 一元线性回归预测法解题程序。第一，作散点图；第二，分析散点图；第三，计算回归系数a、b，得回归方程式=a+bx；第四，检验用一元线性回归方程式的可靠性；第五，预测。

⑤ 用一元线性回归法预测铁路货运量。2006—2018 年某铁路局集团公司吸引范围内煤炭产量和铁路煤炭运量如表 1.3.4 所示。若 2022 年计划煤炭产量为 4.48 亿t，用一元线性回归预测法预测该局2022年煤炭运输量。

表1.3.4　一元线性回归计算表　单位：亿t

第一步，作散点图，如图1.3.2所示。

第二步，从散点图看煤炭运输量随吸引区煤炭产量增加，呈上升趋势，说明可以用趋势线=a+bx来描述它。

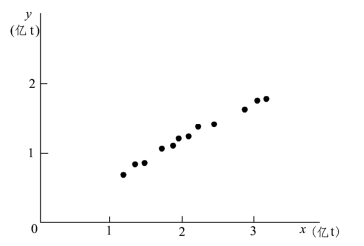
图1.3.2　散点图

第三步，计算回归系数a、b。为便于计算，应用煤炭运量与煤炭产量相关计算表，如表1.3.4所示。

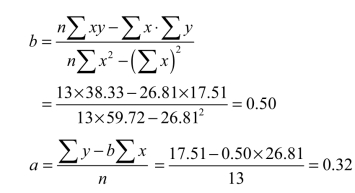
得预测回归方程式：

第四步，检验用一元线性回归方程式的可靠性。

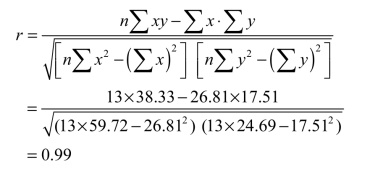
查相关系数显著性检验表，n=13，n－2 =11，r0.05=0.553，r0.01=0.684，而0.99＞0.684，说明铁路煤炭运量与煤炭产量在α=0.01水平上相关显著。

第五步，预测2022年煤炭运输量。

2022年煤炭产量为4.84亿t时，铁路局集团公司煤炭运输量为：