投入产出结构分解分析详解

投入产出分析，是基于国家或地区投入产出表（IO 表），研究经济系统内部各个部门间相互依存关系的数量经济分析工具。国家IO 表反映了产品和服务的流动，以及在一个经济体中的沿着供应链的生产者和消费者之间的相互依存关系（Miller 和Blair，2009；Murray 和Wood，2010）。由于投入产出分析可以通过分析整体供应链来研究经济系统的运行情况，因此其也可以作为一项用来研究电力投入的有效分析工具。按照国家统计局公布的全国IO 表，一个包含n 个部门、k 种最终使用的非竞争型电力投入产出模型如下：

其中，e=E//X，，

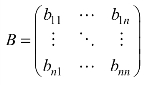
其中，E 是k 维列向量，代表由最终使用通过国内行业供应链引致的各部门的电力投入；e 是n 维电力强度（Electricity Intensity）列向量，其中ie 表示第i 部门每单位总产出的用电量；X 为n 维总产出列向量，其中 xj代表第j部门的总产出；A 为n×n 直接消耗系数矩阵，其中 aij表示第j 部门生产单位产品对第i 部门产品的直接消耗量；F 为n×k 最终使用矩阵，其中 fim代表第m 类最终使用对第i 部门产品的使用量（i∈{1，…，n}，m∈{1，…，k}）；B为n×n 列昂惕夫逆矩阵（Leontief Inverse Matrix），其中 bij代表第j 产品部门增加一个单位最终使用时，对第i 产品部门的完全需要量（i、j ∈{1，…，n}）；1u 为k 维列向量，其中的元素均为1。

参照 Dietzenbacher 和 Los（1998）、Meng 等基于两种极分解（Polar Decomposition）的平均值结构分解分析法，本文的分解过程如下：

其中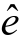 为n×n 电力强度对角矩阵；由以上等式我们可知，基准期（t0）和计算期（t1）的用电量变化量（ΔE），首先可以被分解为跟电力强度变化量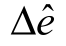（）、列昂惕夫逆矩阵变化量（ΔB）、最终使用矩阵变化量（ΔF）相关的三个多项式，即式（2.1）至式（2.3）。

其次，由于如下等式恒成立，列昂惕夫逆矩阵变化量（ΔB）又可以用直接消耗系数矩阵变化量（ΔA）来进行替换^[2]：

进一步，投入产出系统中的最终使用可以进行如下分解：

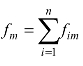其中，u2是每个元素都为1 的n 维行向量；n×k 矩阵，其中为第m 类最终使用的总支出（，m=1，…，k）中对第i部门产品支出的比例，P代表的是最终使用结构；k×k 矩阵，代表的是各类使用总量。(www.xing528.com)

此外，计算期最终使用结构矩阵（Pt1）可以表示为基准期最终使用结构矩阵（Pt0）和最终使用结构变化矩阵（ΔP）之和，即

令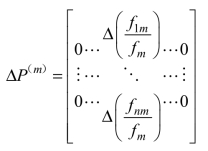代表第m 类最终使用结构的变化量，上角标“m”表明最终使用结构变化矩阵第m 列发生变化。

因此有

同理，

最后，将式（3）至式（6）带入式（2）中，进一步结构分解可得到如下等式：

用电量变化量（ΔE）可以进一步分解为以下五部分：（1）多项式（7.1），即，代表电力强度变化量引起的电力投入变化；（2）多项式（7.2），即，表示直接消耗系数矩阵变化量（ΔA，代表技术—投入结构变化）带来的电力投入变化；（3）多项式（7.3），即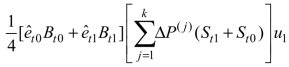，代表对不同部门产品的最终使用结构变化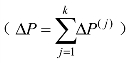带来的电力投入变化，本文的最终使用分类包括农村居民消费支出、城镇居民消费支出、政府消费支出、固定资本形成总额、存货增加、出口这6 项；（4）多项式（7.4），即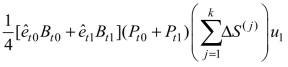，代表各类使用总量（ΔS）带来的电力投入变化。整个结构分解过程可以用图1来表示。

图1　用电量变化的结构分解