机场λ值对航班延误扩散的影响分析

1.仿真系统的构建

下文就机场λ值的大小对航班延误扩散的影响作仿真分析。已知延误航班所在机场的其他航班是否会受到初始延误扩散的影响，取决于机场的延误扩散系数λ。在仿真研究中，将根据实际情况中λ对航班扩散的不确定性，运用Excel软件，使用函数“SUMIF=RAND()”在区间（0，1）范围内生成随机数，再将随机数与λ值作比较。若“随机数＞λ值，则航班不受延误扩散的影响”；若“随机数＜λ值，则航班受到延误扩散的影响，发生延误”。具体方法如后文中的仿真计算过程。

现假定其他飞行资源不影响航空网络中航班延误的扩散，将机场的λ值作为唯一影响航班延误扩散的变量，建立由10个机场组成的航空网络模型，如图7-9所示。在该模型中，所有机场的λ值大小相等；且当发生延误时，同延误机场连接的每条航线各有2个航班准备从延误机场起飞。

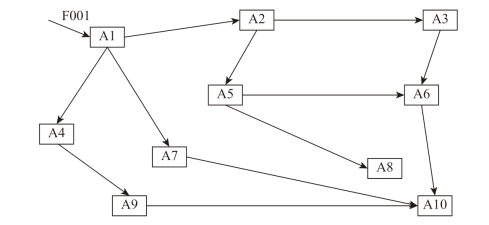
图7-9　基于机场λ值为唯一变量建立的由10个机场组成的航空网络模型

2.仿真结果计算

以图7-9中基于机场λ值为唯一变量建立的由10个机场组成的航空网络模型为例，当航班F001到达延误时间为T（T为大于15的定值）时，机场A1出现初始延误。分别计算当λ值为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9时，整个航空网络的延误情况。

当λ=0.1时，延误在机场A1的扩散情况如下：

航线A1、A2上的两个航班的随机数分别是0.2364、0.4967。二者均大于λ，两个航班均未受到延误的扩散影响，所以延误未经航线A1、A2扩散到机场A2。

航线A1、A4上的两个航班的随机数分别是0.8255、0.5610。二者均大于λ，两个航班均未受到延误的扩散影响，所以延误未经航线A1、A4扩散到机场A4。

航线A1、A7上的两个航班的随机数分别是0.8754、0.7700。二者均大于λ，两个航班均未受到延误的扩散影响，所以延误未经航线A1、A4扩散到机场A4。

此时，由航班F001造成的初始延误没有经过机场A1扩散到其他航班，整个网络没有延误扩散现象。延误机场1个，延误总时间T，延误航班的平均延误时间T。

同λ=0.1的仿真原理，演算出不同的λ值对整个航空网络的延误扩散的仿真结果，并汇总如表7-3所示。

表7-3　以λ为唯一变量的航空网络延误扩散的仿真结果(www.xing528.com)

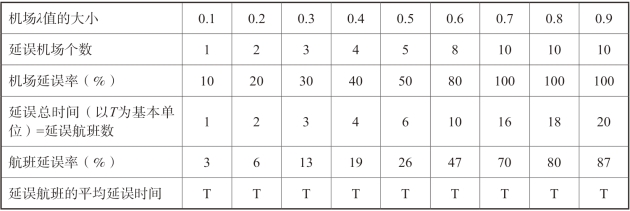
3.仿真结果分析

（1）机场λ值的大小对航班延误扩散造成航班延误的机场个数的影响

从表7-3可以得出机场λ值的大小与整个航空网络延误机场率之间的数量关系，如图7-10所示。

图7-10　机场λ值的大小与整个航空网络延误机场率之间的数量关系

从图7-10中的机场λ值的大小与整个航空网络的延误机场率的数量关系的5组数据可以看出，λ值的大小与延误机场数量有一定的正相关关系。由于0＜λ＜1，当λ趋近于0时，发生延误扩散的机场数量就趋近于0；当λ在0到0.7时，延误机场数量呈向上抛物线形式增长；当λ大于0.7时，延误机场数量就趋近于整个航空网络的全部机场数量。

（2）机场λ值的大小对整个航空网络的总延误时间的影响

从表7-3可以得出，机场λ值与整个航空网络延误总时间的关系，如图7-11所示。

图7-11　机场λ值的大小与整个航空网络的延误总时间的数量关系

从图7-11中的机场λ值的大小与整个航空网络的延误总时间的数量关系的5组数据可以看出，λ值的大小与延误总时间有一定的正“S”曲线关系。由于0＜λ＜1，当λ趋近于0时，延误总时间就趋近于0；当λ在0到0.5时，延误总时间随着λ的增大而缓慢增加；当λ值在0.5到0.7时，延误总时间随λ的增大而急速增加；当λ值在0.7与趋近于1时，延误总时间缓慢增加，并趋于一个定值。

（3）机场λ值的大小对延误航班的平均延误时间的影响

从表7-3可以得出，在该航空网络模型中不考虑其他飞行资源的情况下，机场λ值对延误航班的平均延误时间的影响是一个定值，且该值等于初始延误时间。也就是说无论λ的大小如何变化，它只能影响到延误是否对其他航班造成扩散影响，以及整个航空网络的延误扩散情况。