初始延误时间对航班延误扩散的影响分析：一项研究

1.仿真系统的构建

为控制其他变量，下面将建立一个由单架飞机在5个机场之间执行5个航班的封闭环状的航空网络模型。在该模型中，仅考虑飞机作为唯一的航班延误扩散方式，其他资源对航班延误扩散的影响不计。这5个航班分别是F001、F002、F003、F004、F005。该模型示意图如图7-1所示。

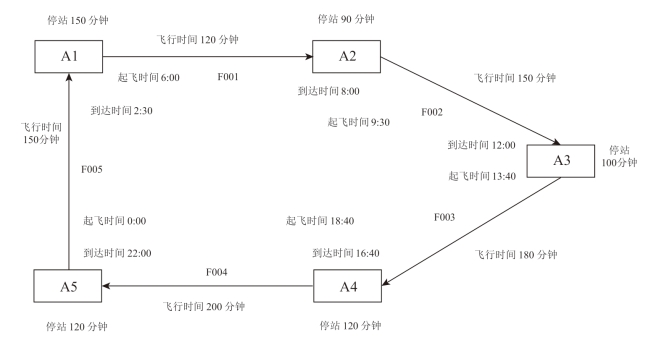
图7-1　单架飞机在5个机场之间执行5个航班的封闭环状的航空网络模型示意图

2.仿真结果计算

以图7-1中单架飞机执行5个航班飞行情况为例，飞机在5个机场的最小周转时间为55分钟，延误认定时间为15分钟。现在将航班F001的初始延误时间视为唯一变量的情况下，演算仿真航班的延误波及情况。

（1）假设“航班F001起飞初始延误时间为60分钟”，则后续航班的延误情况如下所示：

① 航班在机场A2的延误情况分析。

由于航班F001的实际起飞时间为7:00，飞行时间为120分钟，初始延误时间为60分钟，则航班到达机场A2的实际时间为9:00。

由于后续航班F002仍需使用同一架飞机，且其起飞时间为9:30，停站时间为90分钟，最小周转时间为55分钟，则该航班的松弛时间为90-55=35分钟。由于初始延误时间（60分钟）＞松弛时间（35分钟）+延误认定时间（15分钟），则该航班将受到上一航班影响，发生延误，其延误时间=初始延误时间（60分钟）-松弛时间（35分钟）=25分钟

② 航班在机场A3的延误情况分析。

同理，由于航班F002的实际起飞时间为9:55，飞行时间为150分钟，初始延误时间为25分钟，则航班到达机场A3的实际时间为12:25。

初始延误时间（25分钟）＜松弛时间（45分钟）+延误认定时间（15分钟），则该航班不受上一航班的影响，未发生延误。

小结：当航班F001发生起飞初始延误为60分钟时，航班F001、F002分别延误60、25分钟，航班F003、F004、F005正常起降，总延误时间为85分钟，发生延误的机场有A1、A2。

（2）分别假设“航班F001起飞初始延误时间为120、180、240分钟”。根据以上仿真分析步骤，计算后续航班的延误情况，并将仿真结果汇总，如表7-1所示。

表7-1　各个机场延误扩散仿真结果汇总　时间单位：分钟　

(www.xing528.com)

3.仿真结果分析

（1）初始延误时间对航班延误扩散造成航班延误的机场个数的影响

根据表7-2 可以得出初始延误时间与延误机场数之间的对应关系，如图7-2所示。

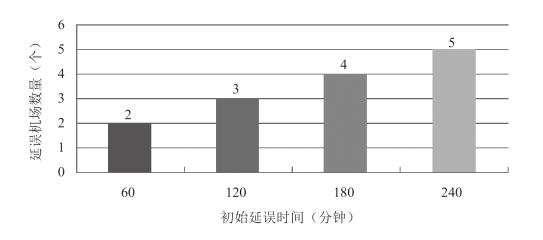
图7-2　初始延误时间与受到延误扩散机场的数量关系

根据图7-2中的4组仿真数据可以看出，初始延误时间与受到延误扩散的机场个数之间存在着正相关关系，也就是说，初始延误时间越长，受到延误扩散的机场就越多；反之亦然。

（2）初始延误时间对整个航空网络的总延误时间的影响

根据表7-2可以得出初始延误时间与整个航空网络的总延误时间（不计初始延误时间）之间的对应关系，如图7-3所示。

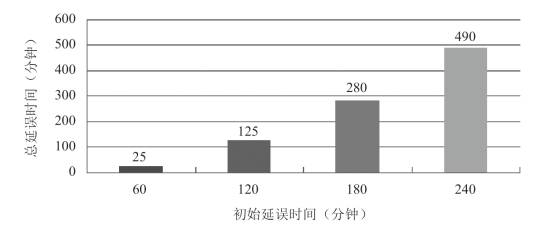
图7-3　初始延误时间与整个航空网络的总延误时间的数量关系

根据图7-3中的4组仿真数据可以看出，初始延误时间与整个航空网络的总延误时间之间存在着正相关关系。也就是说初始延误时间越长，整个航空网络的总延误时间就越长；反之亦然。

（3）初始延误时间对延误航班的平均延误时间的影响

根据表7-2可以得出初始延误时间与延误航班的平均延误时间（不计未发生延误的航班）之间的对应关系，如图7-4所示。

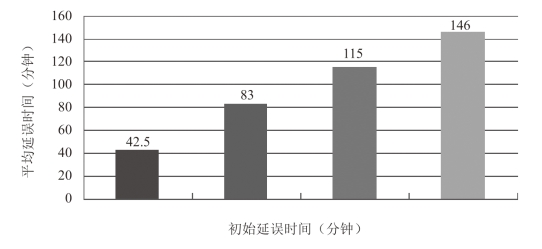
图7-4　初始延误时间与延误航班的平均延误时间的数量关系

根据图7-4中的4组仿真数据可以看出，初始延误时间与延误航班的平均延误时间（不计未发生延误的航班）之间数量关系还是正相关。也就是说，初始延误时间越长，延误航班的平均延误时间就越长；反之亦然。