网络个体特征指标可以用来度量节点城市个体的发展状况与其在网络中影响力的大小。本文对城市节点的度中心性、邻近中心性、介中心性等个体特征指标进行了测度。
1.度中心性
节点的度中心性有两种:绝对度中心性和相对度中心性。
(1)绝对度中心性
节点的度中心性表示有多少节点会与任一节点i有联系,也表示有多少边会与节点i相连,记为:
![]()
(2)相对度中心性
由于不同网络的中心性不能相互比较,所以弗里曼(Freeman,1979)提出了对绝对中心性进行标准化,即用点的绝对中心性除以网络中最大可能的度数。
考虑网络规模后的标准化度中心性为:

其中ki表示节点i的度,n表示网络中节点的数量。
度中心性是在网络分析中刻画节点中心性的最直接度量指标,它反映出网络中某一节点是否有可能与其他节点直接相连。一个节点的节点度越大就意味着这个节点的度中心性越高,该节点在网络中的地位就越高。
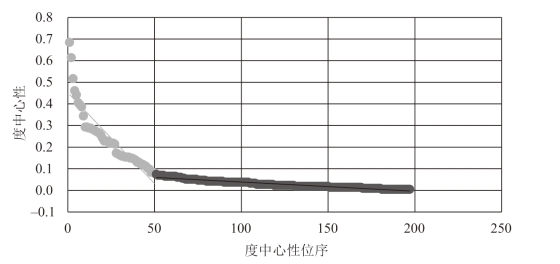
图3-7 度中心性分布示意图
借助复杂网络专业分析软件Ucinet,利用邻接矩阵A,计算得到216座城市节点的度中心值,并据此作出度中心性的分布示意图,如图3-7所示。经过分析发现,有197个节点城市的度中心值不为0。对以城市为节点的中国航空网络的度中心性进行分析,我们发现:度中心性的最大值为0.68(北京),最小值仅0.004(包括阿里、阿拉善右旗、德令哈等17个城市),最大值与最小值二者的度中心值差距达到170倍,由此可见,在中国城市航空网络中,不同的节点所连接的航段数量间有比较大的差距。
度中心性的三层等级结构体系如表3-5所示。其中,第一层次和第二层次在中国航空网络体系中具有枢纽作用,北京、上海与广州三个城市的度中心性明显高于其他城市,并且仅仅三个城市的航线总和就占据了全部航线的12.3%,构成了中国航空网络的顶层枢纽体系。按照中心性变化的趋势,第三层级结构中的城市大体又可以分为两类:第一类的城市度中心值介于0.05~0.35,这类城市的度值在11~49,包括呼和浩特、兰州、郑州等54个城市;另一类则为度中心值低于 0.05的城市,这类城市的度值小于10,包括毕节、淮安、井冈山等154个城市。
表3-5 度中心性的三层等级结构体系

2.邻近中心性(https://www.xing528.com)
邻近中心性定义为任一节点i与其他所有节点相连的最短路径的和,记为:

考虑网络规模后得到的标准化邻近中心性为:

dij表示从节点i到j的最短距离;在航空网络中,即考虑为所需要中转的最少次数。n-1不仅表示网络规模,同时还表示网络中最大可能的度数。
对邻近中心性进行标准化,则有0≤Cc(i)≤1;Cc(i)。其值越大,节点的邻近中心性越强。
借助复杂网络专业分析软件Ucinet,利用邻接矩阵X,计算得出中国城市航空网络中204个城市节点的邻近中心性,并据此作出邻近中心性的分布示意图,如图3-8所示。在航空网络中,邻近中心性有其更为具体的含义,它指城市节点与节点之间在网络中的可访问性,也可以诠释城市节点到其他节点的快慢程度,也可以度量资源共享速度的快慢。对图3-8邻近中心性分布示意图进行分析可知,在邻近中心性值不为0的197个节点城市中,邻近中心值最大的城市为沈阳(0.04943),邻近中心值最小为0.04502,二者邻近中心值的差距较小,可见节点邻近中心性的差距不如度中心性明显,节点整体的可访问性较好,网络结构的“小世界效应”提高了其连通效率和资源共享速度。

图3-8 邻近中心性分布示意图
3.介中心性
节点i的介中心性定义为网络中所有节点之间的最短路径中经过节点i的数量,记为:

其中bjk(i)表示点j和k之间的最短路径经过节点i上的实际数量与最大可能数量的比值。
考虑网络规模后的标准介中心性为:

Freeman(1978,1979)证明了节点的最大介数为(n-1)(n-2)/2,因而有0<CB(i)<1。该值越大,表明介中心性越大,在本文中城市节点的介中心性反映了该城市节点在航空网络中的中转和衔接功能。
借助复杂网络专业分析软件Ucinet,利用邻接矩阵X,计算得出中国城市航空网络中204个城市节点的邻近中心性,并据此作出介中心性的分布示意图,如图3-9所示。对以城市为节点的中国航空网络的介中心性进行分析发现,介中心值最大为北京(0.182),最小值为0。在100个介中心城市不为0值的城市中,只有7个城市的介中心值大于0.04,仅占7个百分点。尽管介中心值的绝对差异较小,但相对差异较为明显,排在第一位的城市北京(0.182)的介中心值是第二位城市上海(0.126)的1.44倍,是第三位城市广州(0.067)的2.71倍。

图3-9 介中心性分布示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




