随机网络的拓扑结构及局限性分析

随机网络中两个节点之间边的连接与否不是确定的事情，而是根据一个概率决定。从1959年匈牙利数学家Erdos和Alfred Renyi提出了ER随机网络模型开始，它在接下来的40多年里一直被很多科学家认为是描述真实系统最适宜的网络。但这种方法是静态的，对于普遍存在的动态的演化系统显然不能进行分析研究。在传统的随机网络（如ER模型）中，由于各个节点之间的连接是随机的，因此整个网络是均匀的，大部分节点的连接数目大致相同，也就是大多数节点的度大致相等，接近于网络的平均度〈k〉。度分布服从泊松（Poisson）分布，这个泊松分布在P（〈k〉）达到峰值，网络中大多数节点的度都集中在其附近，说明节点有同质性，如图2-3所示。

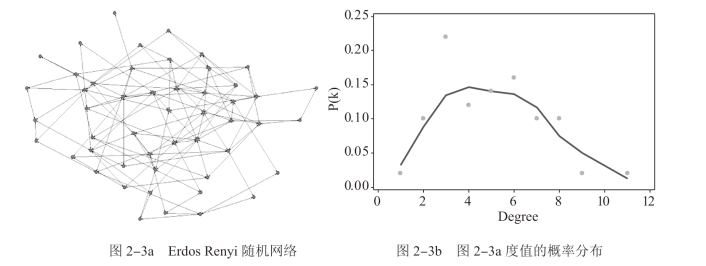
图2-3　Erdos Renyi随机网络及度值的概率分布（50个节点，平均度 =4.92）

在随机网络中连接数目比平均数高许多或低许多的节点都极少，随着连接数的增大，其概率呈指数形式迅速递减。故随机网络亦称指数网络。

随机网络的特点包括：(www.xing528.com)

① 度分布：在平均度达到峰值，但是以指数形式衰减。

② 同质性：每一个节点都有大致相同的连接数。

③ 随机网络具有小的簇系数和小的平均距离。

大量社会科学、生物和计算机科学的实证研究表明，通常的随机网络范式往往不能很好地描述现实的网络。虽然随机网络的平均路径长度短，和许多实证研究的结果一致，但是在真实网络中，平均簇系数很大，而如上所说，随机网络的平均簇系数却小。因此，随机网络不能很好地刻画现实网络。

从网络的拓扑结构及度分布情况看，均匀网络与随机网络均较为接近。但二者之间存在本质的区别：随机网络中节点与边是通过相关算法随机生成的，其只能作为复杂网络的基本模型之一，在现实世界中不存在随机网络；而均匀网络是现实世界中存在的复杂网络，现实世界中只存在均匀网络而不存在随机网络。