二阶段最小二乘法：详解2SLS法

（一）2SLS法的基本思想

间接最小二乘法只适用于恰好识别的结构方程。工具变量法对于恰好识别的结构方程是有效的。但对过度识别方程虽然能够给出过度识别结构方程的参数估计，但这种方法不是有效的。其原因在于选择工具变量的任意性和失去了未被选用的前定变量所提供的信息。对一个特定的内生变量，究竟选择哪个前定变量作为工具变量最为适当，并无一个可遵循的准则。那么如何解决在模型中选取前定变量来构造内生说明变量的工具变量呢？

一个很自然的想法是，如果模型中每个内生说明变量的工具变量都在前定变量中选取，那么工具变量的最普遍的形式便是模型中所有前定变量的线性组合，也就是我们可以利用间接最小二乘法对约简型方程估计式作为工具变量。因为这些估计式是模型中全部前定变量的线性组合，作为工具变量蔓用了全部前定变量的观测值，这就解决了选择工具变量的唯一性和最合理的问题。所谓合理就指工具变量与它所代表的内生说明变量相关性最强。

（二）二阶段最小二乘法的步骤

设有结构模型

其中，Y1、Y2是内生变量，X1，X2是外生变量。

第一阶段，写出结构模型（10-71）对应的约简型

对约简型的每个方程应用OLS法，得

于是有

其中，ε1t，ε2t分别为υ1t，υ2t的OLS估计量。

第二阶段

将（10-74）代入被估计的结构方程（10-73）的右边的内生变量。

其中，

对模型（10-75）中每一个方程分别应用OLS法，得出结构参数的估计值，便是二阶段最小二乘估计量。在计算时需要用到的估计值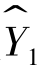 和，应通过（10-73）算出。由于这个方法是在二个阶段分别应用最小二乘法，故叫作二阶段最小二乘法。

在实际应用二阶段最小二乘法时，第一阶段对约简型方程应有OLS法只需求出我们所需要的，并不需要求出εit的值。第二阶段只需用代替所估计方程右边的Yit即可应用OLS法，只不过这里的εit*已不是原来uit罢了。(www.xing528.com)

综上所述，二阶段最小乘法第一阶段的任务是产生一个工具变量。第二阶段的任务是通过一种特殊形式的工具变量得出结构参数的一致估计量。

（三）应用二阶段最小二乘法应当满足的假设条件

1.被估计的结构方程必须是可识别的。

2.结构方程中的随机扰动项必须满足经典回归分析的基本假定；零均值、等方差、无自相关并且与所有前定量协方差为零。由于约简式方程随机扰动项是结构方程随机扰动项的线性结合，因而约简式方程随机扰动项也满足上述假定。

3.所拟定模型的全部前定变量必须是正确设定的，并且前定变量之间不存在高度多重共线。

4.假定样本容量足够大，至少观察值的数目必须大于前定变量的数目，以保证约简式的估计量有意义。

（四）小结

1.二阶段最小二乘法是单方程估计法，适用于过度识别的方程，也可用于恰好识别方程，它可以不考虑其他方程，因此对多方程的计量经济模型也很实用。

2.对恰好识别方程，二阶段最小二乘法与间接最小二乘法和工具变量法会得出相同的估计量。

3.二阶段最小乘法是一种特定的工具变量法，它考虑了联立方程系统所有前定量对内生变量的影响，避免了工具变量法用于过度识别方程产生的偏误和不一致性的缺点。

4.二阶段最小二乘法要求样本容量足够大，以保证第一阶段正确估计内生变量的数值，由于我国积累的时间序列数据不长，在宏观模型参数估计时，常常感到数据不足。

5.二阶段最小二乘法的不足之处是它对误差也很敏感。

总的来说，2SLS法是计算容易、花费少的方法，因此估计联立方程系统是应用较广泛的方法。