协整性的检验有两种方法:一种是基于回归残差的协整检验,这种检验也称为单一方程的协整检验;另一种是基于回归系数的完全信息协整检验。这里我们仅考虑单一方程的情形,而且主要介绍两变量协整关系的EG两步法检验。
第一步,若Xt与Yt是一阶单整序列,即ΔXt和ΔYt是平稳的,用OLS法对回归方程(也称为协整回归方程)
![]()
进行估计,得到残差序列![]()
第二步,检验et的平稳性。若et为平稳的,则Xt与Yt是协整的,反之则不是协整的。因为若Xt与Yt不是协整的,则它们的任一线性组合都是非平稳的。因此残差et将是非平稳。换言之,对残差序列et是否具有平稳性的检验,也就是对Xt与Yt是否存在协整的检验。
检验et为非平稳的假设可用两种方法。
一种方法是对残差序列进行DF检验或者ADF检验,即对et进行单位根检验,其检验方法在前面已介绍。一个需要注意的问题是,这里的DF或ADF检验是针对协整回归计算出的误差项et而非真正的非均衡误差ut进行的。而OLS法采用了残差最小平方和原理,因此,估计量是向下偏倚的,这样将导致拒绝零假设的机会比实际情形大。于是对et平稳性检验的DF与ADF临界值应该比正常的DF与ADF临界值还要小。MacKinnon(1991)通过模拟试验给出了协整检验的临界值,表9-7是双变量情形下不同样本容量的临界值。
表9-7 双变量协整ADF检验临界值

(续表)

另一种方法是协整回归DW检验。具体做法为,用协整回归所得的残差构造DW统计量:
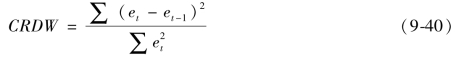 (https://www.xing528.com)
(https://www.xing528.com)
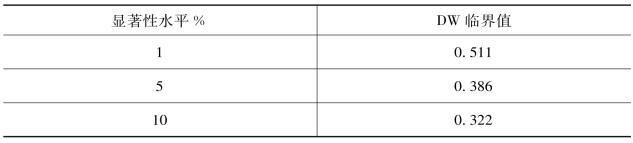
若et是随机游走的,则et-et-1的数学期望为0,故DW也应接近于0。因此,只需检验:H0:DW=0是否成立,若H0成立,et为随机游走,Xt与Yt间不存在协整,反之则存在协整。Sargan和Bhargava最早编制了用于检验协整的DW临界值表。表9-8是观察数为100时,该检验的临界值。例如,当DW=0.71时,在1%的显著性水平上我们能拒绝H0:DW=0,即拒绝非协整假设。
表9-8 检验DW=0的临界值
例9-2 利用表9-6提供的数据探索该市城镇居民消费支出与可支配收入之间的协整关系。
记可支配收入为Xt,消费支出为Yt,由例1可知,Xt为一阶单整序列,同样的步骤可检验Yt也是一阶单整序列。
对总体回归模型Yt=α+βXt+ut进行参数估计的结果见表9-9。
表9-9 第一步回归结果
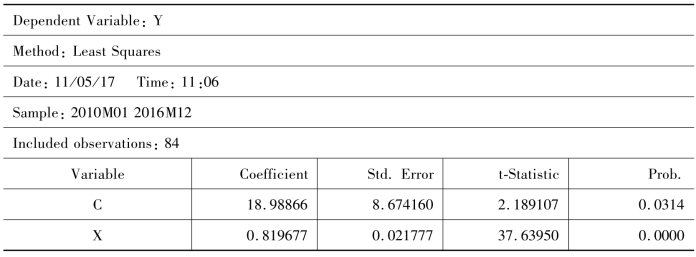
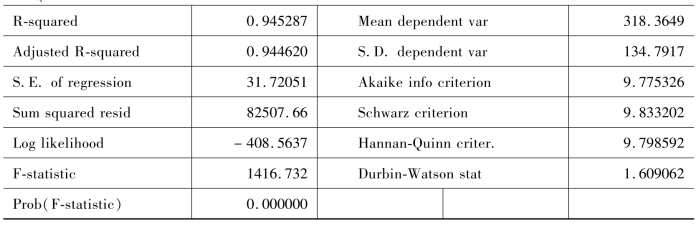
为检验残差序列的平稳性,通过命令:genr e=resid生成新序列e,e即为表9-9样本回归模型对应的残差,由于残差序列均值为0,故此选择无截距项、无趋势项的模型进行检验,残差序列平稳性检验结果如表9-10所示。
表9-10 残差平稳性的检验结果
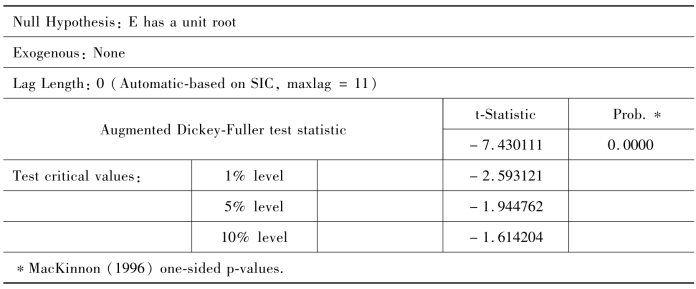
由表9-10可见,ADF统计量观测值为-7.430111,小于1%水平下的临界值,因此,残差序列是平稳的,由此可见,该市2010—2016年各月的消费支出与可支配收入之间存在协整关系。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




