Dickey-Fuller检验（DF检验）

大多数的经济变量，如GDP、总消费、价格水平以及货币供给虽M2等都会呈现出强烈的趋势特征。这些具有趋势特征的经济变量，当发生经济振荡或冲击后，一般会出现两种情形：一是受到振荡或冲击后，经济变量逐渐又回到它们的长期趋势轨迹；二是这些经济变量没有回到原有轨迹，而呈现出随机游走的状态。若我们研究的经济变量遵从一个非平稳过程（比如随机游走过程），当运用最小二乘法时，高斯-马尔科夫定理不再成立，一个变量对其他变量的回归可能会导致伪回归结果。同时，如果所研究的经济变量（如GDP）是非平稳的，则经济出现突发性振荡（如石油价格猛增，金融危机或政府开支骤减等）所造成的影响不会在短期内消失，其影响将是持久性的。这也是研究单位根检验的重要意义所在。在介绍检验方法之前，先讨论检验统计量的分布。

（一）情形1（如图9-5所示）

数据生成过程（DGP）：

OLS估计对应的总体回归模型：

提出假设H0：γ=1；H1：γ＜1

若真值γ=0，则统计量：

的极限分布为标准正态分布。若真值｜γ｜＜1，则统计量：

渐近服从标准正态分布。

在H0成立的条件下γ=1，这时统计量不再服从通常的t分布，而是服从DF分布。此时称为DF统计量。可以证明当T→∞时，

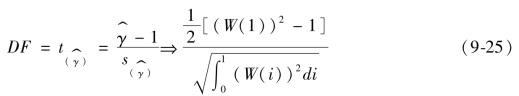
DF统计量是Op（1）的，其渐近分布与σ无关。由于该极限分布无法用解析的方法求解，一般都是用模拟和数值计算的方法研究DF统计量的有限样本分布。

图9-5　在情形1下：T=100，模拟1万次的DF统计量的分布

（二）情形2（如图9-6所示）

数据生成过程（DGP）：

OLS估计对应的总体回归模型为

其原假设为

H0：α=0；γ=1；H1：α≠0；γ＜1；

统计量的极限分布都是Wiener过程的泛函。可以证明，当T→∞时，

不再服从t分布。的极限分布是Wiener过程的泛函。

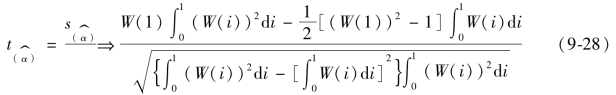
统计量是Op（1）的。

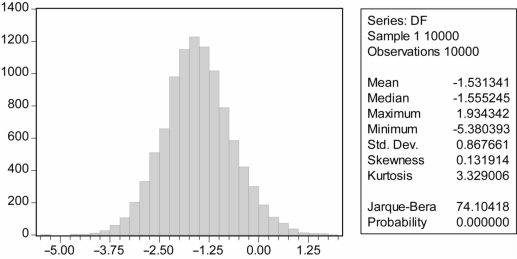
图9-6　在情形2下：T=100，模拟1万次的DF统计量的分布

图9-7　在情形2下：T=100，模拟1万次的^的分布

（三）情形3（如图9-8至图9-10所示）(www.xing528.com)

数据生成过程（DGP）：

OLS估计对应的总体回归模型为

为防止α不为零时从而使估计式引入时间趋势项，导致解释变量多重共线性，等价的总体回归模型为

其中，α*=（1-γ）α，γ*=γ，β*=β+γα

H0：α=α0；γ=1；β=0相当于：H0：α*=0；γ*=1；β*=α0

H1：α≠α0；γ＜1；β≠0

讨论的极限分布和有限样本分布特征。可以证明，当T→∞时，

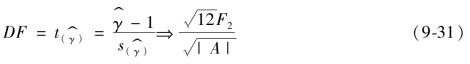
其中

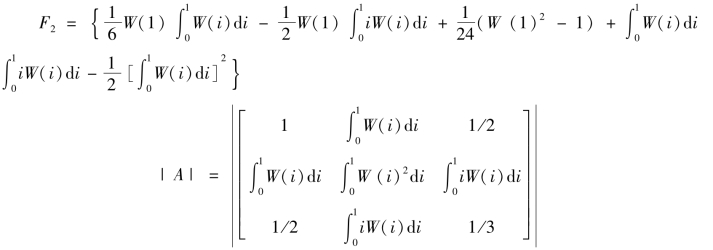
DF统计量是Op（1）的，其渐近分布既不依赖于α，也不依赖于σ。

服从的是如下极限分布。

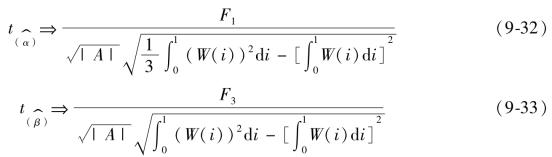
其中，F1和F2都是Wiener过程的泛函。统计量是Op（1）的，其渐近分布既不依赖于α，也不依赖于σ。

γ=-1时DF的分布是γ=1时的DF分布的镜像，所以只研究γ=1条件下DF的分布即可。对于经济问题，很少出现γ=-1的情形。下面我们用图形把DF统计量的有限样本分布特征总结一下。

图9-8　在情形3下：T=100，模拟1万次的DF统计量的分布

图9-9　在情形3下：T=100，模拟1万次的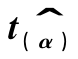的分布

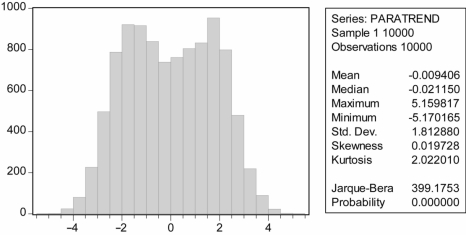
图9-10　在情形3下：T=100，模拟1万次的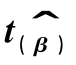的分布

以模型（9-21）为条件，取样本容量T=100，用蒙特卡罗方法，分别用式（9-29）、式（9-26）和式（9-22）各模拟10000次得到的DF的分布见图9-10。黑、蓝、红色直方图分别代表式（9-29）、式（9-26）和式（9-22）中DF统计量的分布。随着确定项的增加，分布越来越向左移。蓝色DF分布近似于t分布，但整体向左大约移动了1.6个单位。（如图9-11所示）

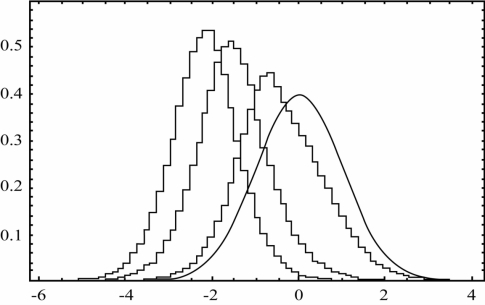
图9-11　情形1、2、3的DF统计量分布的蒙特卡罗模拟（T=50）

因为不同情况，DF统计量分布有区别，所以Fuller（1976）针对如下三种方程编制了临界值表

模型Ⅰ：yt=γyt-1+ut

模型Ⅱ：yt=α+γyt-1+ut

模型Ⅲ； yt=α+βt+γyt-1+ut

Fuller使用蒙特卡罗模拟方法得到的DF统计量的百分位数如表9-2所示。

表9-2　DF分布百分位数表

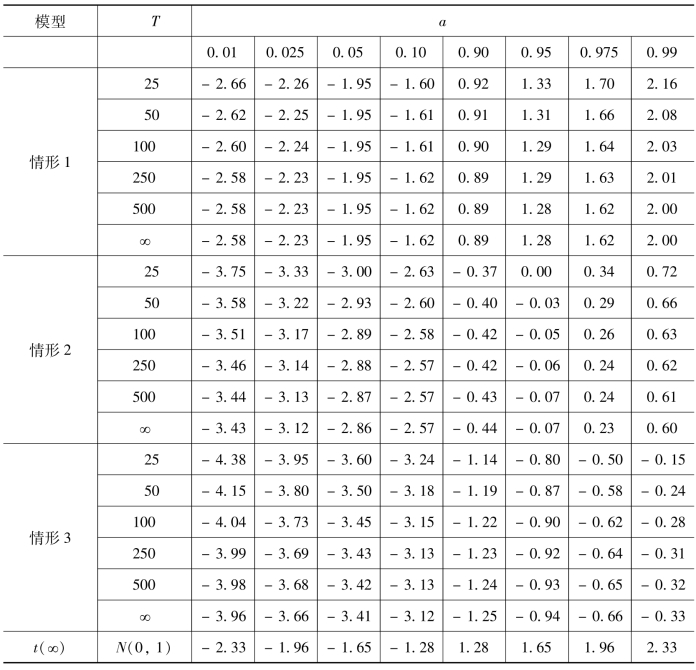
注：适用于情形1、2、3，条件β=1。T：样本容量，α：检验水平。

后来，Mackinnon把临界值表加以扩充，形成了目前使用广泛的临界值表，在EViews软件中使用的是Mackinnon临界值表。