测量误差的影响及应对策略

测量误差包含两方面的内涵：其一是错误理解经济变量内涵，所采用的测量变量不能精确反映经济变量真实含义，例如，利用企业区域集中度作为产业集群水平的测量变量；其二是变量测量过程中由于人为或技术因素的影响，导致变量测量结果与实际情况不完全相符，例如数据调查登记过程中虚报或瞒报数据将会产生登记误差，另外在数据加工处理过程中也可能导致变量测量结果与实际情况不相符，例如，错误的汇总或分组导致的偏差，以及数据修匀加工导致数据与实际情况不符等；这些有关数据的误差统称为测量误差。测量误差既可能是解释变量的测量误差，也可能是被解释变量的测量误差，或者两类变量都具有测量误差。下面分三种情况，讨论测量误差的后果。

（一）被解释变量有测量误差的后果

为说明被解释变量有测量误差时的后果，假设正确的总体回归模型为

其中，Y*i是被解释变量的理论值，亦即被解释变量的真实取值，Xi为解释变量，ui为随机扰动项。由于被解释变量有测量误差，在建立模型时，被解释变量的观测值为Yi=Y*i+εi，这就意味着实际建模中采用的总体回归模型为

其中，vi=ui+εi是一个合成误差项，包含着随机扰动项和被解释变量的测量误差。为简化分析，假设：E（ui）=E（εi）=0，cov（Xi，ui）=0，var（εi）=σ2ε，var（ui）=σ2u即测量误差与随机扰动项的期望为零，测量误差与随机扰动项都满足同方差性。cov（Xi，εi）=0，即解释变量与被解释变量的测量误差不相关。cov（ui，εj）=0（i，j=1…n），即随机扰动项与被解释变量的测量误差不相关。cov（εi，εj）=0（i≠i），cov（ui，uj）=0（i≠i）即测量误差和随机扰动项不存在自相关。

通过模型（8-33），利用OLS进行参数估计可得

由式（8-34）和式（8-35）以及假设条件E（ui）=E（εi）=0易知和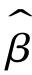仍是α和β的线性无偏估计量。

由var（εi）=σ2ε，var（ui）=σ2u，Cov（ui，εi）=0，可知：var（vi）=σ2ε+σ2u，亦即合成误差项也满足同方差性，由Cov（ui，εj）=0（i，j=1…n），Cov（εi，εj）=0（i≠i），Cov（ui，uj）=0（i≠i）可知：Cov（vi，vj）=0（i≠i），亦即合成误差项不存在自相关。

式（8-34）和式（8-35）以及合成误差项不存在自相关，可得

很显然在被解释变量存在测量误差的情况下，偏回归系数估计量的方差增大，不满足有效性。

易证：

可见，在被解释变量存在测量误差的情况下，是随机扰动项方差σ2n的有偏估计量。

（二）解释变量有测量误差的后果

假设正确的总体回归模型为

其中，X*i为解释变量的真实值，其观测值为Xi假定观测值满足：(www.xing528.com)

ωi为观测误差，且ωi～N（0，σ2ω），那么在进行参数估计时，实际估计的模型为

其中，zi=ui-βiωi，是随机扰动项与解释变量测量误差的合成误差。

假设Cov（ui，ωi）=0，此时：

通过模型（8-40），利用OLS得到的参数估计量为

可以证明，和既不满足无偏性、有效性，也不满足一致性。当样本容量无限增大时，，因此，当解释变量存在测量误差时，OLS估计的结果通常会低估参数真值。

3.解释变量和被解释变量均存在测量误差

假设正确的模型形式为

其中，Y*i、X*i分别为被解释变量和解释变量的实际值，但由于测量误差的存在，解释变量和被解释变量的观测值分别为

假设εi～N（0，σ2ε），ωi～N（0，σ2ω），Cov（εi，Xi）=0，Cov（ui，ωi）=0，Cov（εi，ωi）=0，Yi、Xi分别是Y*i、X*i的测量结果，εi、ωi分别是Y*i、X*i的测量误差，Cov（εi，Xi）=0意味着被解释变量的测量误差与解释变量无关，Cov（εi，ωi）=0意味着被解释变量与解释变量的测量误差无关，同时假定各误差序列没有序列相关。

那么实际采用的总体回归模型为

即对模型（8-47）采用OLS可得

两边求概率极限可得

由于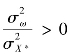，因此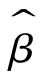不是β的一致估计量，且利用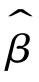容易低估β。

值得注意的是，测量误差属于数据问题，对于计量经济学工作者来讲，只能要求尽可能避免测量误差，希望测量误差足够小，从而不破坏计量分析的合理性，一般往往忽略测量误差问题。