遗漏相关变量的检验优化建议：如何避免遗漏重要变量的检验？

遗漏重要变量有多种检验方法，如DW检验、拉格朗日乘数检验、似然比检验、豪斯曼检验等，本部分内容重点介绍适用于本科教学目的且相关计量经济学软件中常用的检验方法。

（一）DW检验

利用DW检验判断是否遗漏相关变量的基本思想是，认为遗漏的相关变量因模型误设而被包含在了随机扰动项中，那么参数估计所得的残差序列中就包含了遗漏的相关变量对被解释变量条件均值的影响，在线性模型中，解释变量对被解释变量条件均值的影响具有单向性，进而导致在遗漏相关解释变量的模型中残差序列将随着遗漏解释变量的变化而呈现单侧相关性。因此，可以通过残差序列的自相关性检验模型是否遗漏重要解释变量。

从遗漏解释变量模型来看，可以认为遗漏解释变量模型是无遗漏解释变量模型的特例，即被遗漏解释变量对应的偏回归系数为0。例如，模型（8-2）可以视为β3=0条件下的模型（8-1）的特例；称模型（8-1）为无约束回归模型，模型（8-2）为受约束回归模型。

DW检验的具体步骤如下：

1）对设定的模型进行参数估计，得到残差序列ei（i=1…n）；

2）设定H0：无遗漏相关变量（受约束回归模型）H1：遗漏相关变量（无约束回归模型），按照疑似遗漏解释变量递增的顺序对残差序列进行排序，并计算DW统计量观测值，

3）以模型（8-1）和模型（8-2）的分析为例，如果X3是一相关变量，在遗漏相关变量的模型（8-2）中，X3对被解释变量条件均值E（Y/X）的影响β3X3将被包含在残差序列中，那么残差序列将随着X3的增加而呈现出递增或递减的趋势，进而呈现正自相关。因此，通过DW检验后残差序列呈现正自相关，则可以认为模型遗漏相关变量；反之，则认为模型无遗漏相关变量。

仍以例8-1为例，在例8-1中教育支出在地方财政支出中的比重（X6）仅通过t检验被认为是无关变量，那么删除X6后，受约束回归模型为

对其进行参数估计，结果见表8-3。

表8-3　不含X6的回归结果

在进行表8-3的估计时，已经将原始数据按照X6递增的顺序排序，DW统计量的观测值为1.4616，在0.05的显著性水平下，查DW统计量临界值表可知d1=1.160，du=1.735，依据DW检验的决策规则，不存在正自相关，因此，模型（8-26）无遗漏相关变量。仅从模型（8-24）的t检验结果和模型（8-26）的DW检验结果来看，X6确实是无关变量。

（二）拉格朗日乘数检验（LM检验）

拉格朗日乘数检验的基本思想是，模型中遗漏的相关变量包含在随机扰动项中，因此，样本回归模型中的残差项将与相关变量呈现某种统计依存关系，可以将残差序列与疑似相关变量进行回归分析，如果疑似相关变量对残差序列存在显著影响，则认为存在遗漏相关变量偏误，反之，则认为不存在遗漏相关变量偏误。

拉格朗日乘数检验的基本步骤如下：

1）对疑似存在遗漏相关变量的模型（受约束回归模型）进行参数估计，得到残差序列ei（i=1…n）；

2）用残差序列作为被解释变量，对所有解释变量（含疑似遗漏相关变量）进行回归分析，得到辅助回归方程的可决系数R2；

3）设定H0：无遗漏相关变量（受约束） H1：遗漏相关变量（无约束），在大样本情况下构造统计量nR2，恩格尔证明：其中，m为约数个数，在此即为疑似遗漏相关变量个数。

4）如果确实遗漏相关变量，则辅助回归方程将会有较大的可决系数，nR2将会有较大值，因此，此检验为右侧检验，在给定的显著性水平α下，如果nR2＞κ2α（m）则认为无遗漏相关变量不成立，即遗漏相关变量，反之，则认为无遗漏相关变量。

仍以例8-1为例，利用表8-3估计出的残差进行辅助回归分析，结果见表8-4。(www.xing528.com)

表8-4　辅助回归结果

nR2=31×0.119519096461=3.705092，κ20.05（1）=3.84146，则可以认为模型（8-26）没有遗漏相关变量。

（三）一般性检验（RESET）

一般性检验（REGRESSION ERROR SPECIFICATION TESET，RESET）是拉姆齐（Ramsey）于1969年提出的一种检验方法，其基本思想是，如果事先知道遗漏了那个相关变量，只需将此变量引入模型，估计并检验其参数是否显著不为零即可，在是否存在遗漏相关变量偏误的判断中，往往不知道遗漏了哪个变量，这时可寻找一个替代变量Z进行上述检验，在RESET检验中，替代变量Z通常选用设定模型被解释变量拟合值的若干次幂的线性组合。如果设定模型确实存在遗漏相关变量偏误，那么设定模型的残差可用被解释变量拟合值的若干次幂的线性组合显著解释。因此，如果这一线性组合是显著的，则可以认为设定模型存在遗漏相关变量偏误，反之，则不存在遗漏相关变量偏误。

RESET检验的一般步骤如下：

1）对设定模型

采用OLS进行参数估计，得到被解释变量的拟合值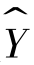和残差序列e，如果残差序列与被解释变量拟合值之间存在某种函数关系，则可以用拟合值的若干次幂的线性组合作为工具变量；

2）在设定模型中加入设定模型拟合值的若干次幂的线性组合，构建辅助回归方程，一般选择的二次方、三次方和四次方的线性组合。

并对上述模型进行参数估计。

3）设定：H0：α1=α2=α3=0，H0：α1、α2、α3不全为零

模型（8-28）相当于给模型（8-29）加上了约束条件α1=α2=α3=0，检验模型（8-28）是否遗漏相关变量，就相当于对模型（8-29）判断约束条件α1=α2=α3=0是否成立，可以用联合F检验进行判断。F检验统计量为

其中，J为约束条件个数，在模型（8-29）下J=3，RSSR为模型（8-28）对应样本回归方程的残差平方和，RSSU为模型（8-29）对应样本回归方程的残差平方和，R2 R和R2

U分别为对应的可决系数。当原假设成立时，

如果原假设成立，模型（8-28）和模型（8-29）等价，RSSR和RSSU不应该有显著差异，如果RSSR显著大于RSSU，则意味着对被解释变量Y的条件均值产生显著影响，模型（8-28）遗漏相关变量。因此，该检验为右侧检验。

仍以例8-1为例，利用RESET检验判断模型（8-26）是否遗漏相关变量，检验结果如表8-5所示。

表8-5　RESET检验结果

F检验的P值为0.3973，在显著性水平0.05下，不能否认原假设成立，因此，可以认为模型（8-26）无遗漏相关变量。